當前位置：試卷中心 > 試卷詳情

2022-2023學年四川省遂寧中學高一（下）期中數學試卷

發布：2024/12/28 7:0:2

一、單選題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

1．已知向量
a
與
b
共線，下列說法正確的是（　　）
A．
a
=
b
或
a
=
-
b
B．
a
與
b
平行
C．
a
與
b
方向相同或相反 D．存在實數λ，使得
a
=
λ
b
組卷：112引用：2難度：0.8
解析
2．已知
cosα
=
1
3
，且
3
π
2
＜
α
＜
2
π
，則tanα的值為（　　）
A．
-
2
2
3
B．
-
2
4
C．
-
2
D．
-
2
2
組卷：196引用：4難度：0.7
解析
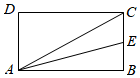3．如圖，在矩形ABCD中，E為BC中點，那么向量
1
2
AD
+
AE
等于（　　）
A．
AB
B．
AC
C．
BC
D．
BE
組卷：324引用：8難度：0.9
解析
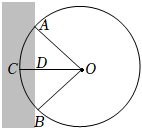4．我國古代數學經典著作《九章算術》中記載了一個“圓材埋壁”的問題：“今有圓材埋在壁中，不知大小，以鋸鋸之，深一寸，鋸道長一尺，問徑幾何？”現有一類似問題，不確定大小的圓柱形木材，部分埋在墻壁中，其截面如圖所示．用鋸去鋸這木材，若鋸口深
CD
=
2
-
3
，鋸道AB=2，則圖中
?
ACB
與弦AB圍成的弓形的面積為（　　）
A．
π
2
-
3
2
B．
2
π
3
-
3
C．
π
3
-
3
2
D．
π
3
-
3
3
組卷：275引用：11難度：0.7
解析
5．已知a=cos1，b=sin2，c=tan4，則（　　）
A．c＞b＞a B．a＞b＞c C．b＞a＞c D．b＞c＞a
組卷：182引用：5難度：0.8
解析
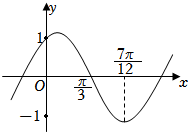6．記函數f（x）=sin（ωx+φ）（其中ω＞0，
|
φ
|
＜
π
2
）的圖像為C，已知C的部分圖像如圖所示，為了得到函數g（x）=sinωx,只要把C上所有的點（　　）
A．向右平行移動
π
6
個單位長度
B．向左平行移動
π
6
個單位長度
C．向右平行移動
π
12
個單位長度
D．向左平行移動
π
12
個單位長度
組卷：171引用：2難度：0.7
解析
7．已知
α
，
β
∈
（
-
π
2
，
π
2
）
，tanα=3，
cos
（
α
+
β
）
=
-
5
5
，則tan（α-β）=（　　）
A．
-
5
2
B．
1
2
C．2 D．
11
2
組卷：163引用：4難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.）

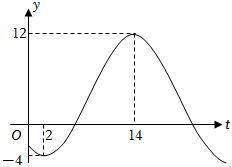21．建設生態文明是關系人民福祉、關乎民族未來的長遠大計．某市通宵營業的大型商場，為響應國家節能減排的號召，在氣溫低于0℃時，才開放中央空調，否則關閉中央空調．如圖是該市冬季某一天的氣溫（單位：℃）隨時間t（0≤t≤24，單位：小時）的大致變化曲線，若該曲線近似滿足f（t）=Asin（ωt-
2
π
3
）+b（A＞0，ω＞0）關系．
（1）求y=f（t）的表達式；
（2）請根據（1）的結論，求該商場的中央空調在一天內開啟的時長．
組卷：194引用：7難度：0.6
解析
22．在△OAB的邊OA、OB上分別有一點P、Q，已知
|
OP
|
：
|
PA
|
=1：2，
|
OQ
|
：
|
QB
|
=3：2，連接AQ、BP，設它們交于點R，若
OA
=
a
，
OB
=
b
．
（Ⅰ）用
a
與
b
表示
OR
；
（Ⅱ）過R作RH⊥AB，垂足為H，若|
a
|=1，|
b
|=2，
a
與
b
的夾角
θ
∈
[
π
3
，
2
π
3
]
，求
|
BH
|
|
BA
|
的范圍．
組卷：254引用：5難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． a = b 或 a = - b	B． a 與 b 平行
C． a 與 b 方向相同或相反	D．存在實數λ，使得 a = λ b

2022-2023學年四川省遂寧中學高一（下）期中數學試卷

一、單選題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

1．已知向量a與b共線，下列說法正確的是（ ）

2．已知cosα=13，且3π2＜α＜2π，則tanα的值為（ ）

3．如圖，在矩形ABCD中，E為BC中點，那么向量12AD+AE等于（ ）

5．已知a=cos1，b=sin2，c=tan4，則（ ）

6．記函數f（x）=sin（ωx+φ）（其中ω＞0，|φ|＜π2）的圖像為C，已知C的部分圖像如圖所示，為了得到函數g（x）=sinωx,只要把C上所有的點（ ）

7．已知α，β∈（-π2，π2），tanα=3，cos（α+β）=-55，則tan（α-β）=（ ）

四、解答題（本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.）

22．在△OAB的邊OA、OB上分別有一點P、Q，已知|OP|：|PA|=1：2，|OQ|：|QB|=3：2，連接AQ、BP，設它們交于點R，若OA=a，OB=b．（Ⅰ）用a與b表示OR；（Ⅱ）過R作RH⊥AB，垂足為H，若|a|=1，|b|=2，a與b的夾角θ∈[π3，2π3]，求|BH||BA|的范圍．

1．已知向量
a
與
b
共線，下列說法正確的是（　　）

2．已知
cosα
=
1
3
，且
3
π
2
＜
α
＜
2
π
，則tanα的值為（　　）

3．如圖，在矩形ABCD中，E為BC中點，那么向量
1
2
AD
+
AE
等于（　　）

5．已知a=cos1，b=sin2，c=tan4，則（　　）

6．記函數f（x）=sin（ωx+φ）（其中ω＞0，
|
φ
|
＜
π
2
）的圖像為C，已知C的部分圖像如圖所示，為了得到函數g（x）=sinωx,只要把C上所有的點（　　）

7．已知
α
，
β
∈
（
-
π
2
，
π
2
）
，tanα=3，
cos
（
α
+
β
）
=
-
5
5
，則tan（α-β）=（　　）