當前位置：試卷中心 > 試卷詳情

2023年福建省寧德市五校教學聯合體蕉城區等4地高考數學質檢試卷（3月份）

發布：2024/10/29 8:0:2

一、單選題。

1．集合A={x|y=
x
2
+
x
-
6
}，
B
=
{
x
|
x
-
a
-
2
x
-
a
≤
0
}
，若A∩B={x|2≤x≤3}，則a的值為（　　）
A．0 B．1 C．2 D．3
組卷：78引用：1難度：0.7
解析
2．已知復數
x
+
yi
1
+
i
=2+i,x,y∈R，則x+y=（　　）
A．2 B．3 C．4 D．5
組卷：269引用：4難度：0.7
解析
3．已知
sin
（
45
°
+
α
）
=
5
5
，
45
°
＜
α
＜
135
°
，則cosα的值為（　　）
A．
3
10
10
B．
-
3
10
10
C．
10
10
D．
-
10
10
組卷：201引用：1難度：0.8
解析
4．恩格爾系數
n
=
食品消費支出總額
消費支出總額
×
100
%
，國際上常用恩格爾系數n來衡量一個地區家庭的富裕程度，恩格爾系數越低，人民生活越富裕．某地區家庭2021年底恩格爾系數n為50%，剛達到小康，預計從2022年起該地區家庭每年消費支出總額增加30%，食品消費支出總額增加20%，依據以上數據，預計該地區家庭恩格爾系數n滿足30%＜n≤40%達到富裕水平，至少經過（　　）年．（參考數據：lg0.6≈-0.22，lg0.8≈-0.10，lg12≈1.08，lg13≈1.11）
A．8年 B．7年 C．4年 D．3年
組卷：135引用：5難度：0.6
解析
5．如圖，圓O半徑為1，圓外一點P到圓心O的距離為2，過P引圓O的兩條切線，切點分別記為A、B，M為圓O上的一個動點，則
PA
?
PM
的最小值為（　　）
A．
3
-1 B．3-
3
C．
3
2
D．
3
組卷：384引用：2難度：0.6
解析
6．已知雙曲線C：
x
2
12
-
y
2
4
=1，點F是C的右焦點，若點P為C左支上的動點，設點P到C的一條漸近線的距離為d,則d+|PF|的最小值為（　　）
A．
2
+
4
3
B．
6
3
C．8 D．10
組卷：108引用：2難度：0.7
解析

7．如圖1所示，四邊形ABCD是邊長為2的正方形，點E、F、M分別為線段BC、CD、BE的中點，分別沿AE、AF及EF所在直線把△AEB，△AFD和△EFC折起，使B、C、D三點重合于點P，得到如圖2所示的三棱錐P-AEF，則下列結論中正確的有（　　）

A．點P在平面AEF上的投影為△AEF的外心

B．直線AM與平面PEF所成角的正切值為2

C．三棱錐P-AEF的內切球半徑為

D．過點M的平面截三棱錐P-AEF的外接球所得截面的面積的取值范圍為

[

，

]

組卷：213引用：1難度：0.5

解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題。

21．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的離心率為
2
2
，過點
（
-
1
，
2
2
）
．
（1）求橢圓C的標準方程；
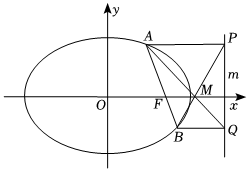
（2）設橢圓的右焦點為F，定直線m：x=2，過點F且斜率不為零的直線l與橢圓交于A，B兩點，過A，B兩點分別作AP⊥m于P，BQ⊥m于Q，直線AQ、BP交于點M，證明：M點為定點，并求出M點的坐標．
組卷：238引用：2難度：0.5
解析
22．已知函數f（x）=e^x+2ax-1，其中a為實數，e為自然對數底數，e=2.71828?．
（1）已知函數x∈R，f（x）≥0，求實數a取值的集合；
（2）已知函數F（x）=f（x）-ax²有兩個不同極值點x₁、x₂，證明
2
a
（
x
1
+
x
2
）
＞
3
x
1
x
2
．
組卷：127引用：2難度：0.2
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2023年福建省寧德市五校教學聯合體蕉城區等4地高考數學質檢試卷（3月份）

一、單選題。

1．集合A={x|y=x2+x-6}，B={x|x-a-2x-a≤0}，若A∩B={x|2≤x≤3}，則a的值為（ ）

2．已知復數x+yi1+i=2+i,x,y∈R，則x+y=（ ）

3．已知sin（45°+α）=55，45°＜α＜135°，則cosα的值為（ ）

5．如圖，圓O半徑為1，圓外一點P到圓心O的距離為2，過P引圓O的兩條切線，切點分別記為A、B，M為圓O上的一個動點，則PA?PM的最小值為（ ）

6．已知雙曲線C：x212-y24=1，點F是C的右焦點，若點P為C左支上的動點，設點P到C的一條漸近線的距離為d,則d+|PF|的最小值為（ ）

7．如圖1所示，四邊形ABCD是邊長為2的正方形，點E、F、M分別為線段BC、CD、BE的中點，分別沿AE、AF及EF所在直線把△AEB，△AFD和△EFC折起，使B、C、D三點重合于點P，得到如圖2所示的三棱錐P-AEF，則下列結論中正確的有（ ）

四、解答題。

22．已知函數f（x）=ex+2ax-1，其中a為實數，e為自然對數底數，e=2.71828?．（1）已知函數x∈R，f（x）≥0，求實數a取值的集合；（2）已知函數F（x）=f（x）-ax2有兩個不同極值點x1、x2，證明2a（x1+x2）＞3x1x2．

1．集合A={x|y=
x
2
+
x
-
6
}，
B
=
{
x
|
x
-
a
-
2
x
-
a
≤
0
}
，若A∩B={x|2≤x≤3}，則a的值為（　　）

2．已知復數
x
+
yi
1
+
i
=2+i,x,y∈R，則x+y=（　　）

3．已知
sin
（
45
°
+
α
）
=
5
5
，
45
°
＜
α
＜
135
°
，則cosα的值為（　　）

5．如圖，圓O半徑為1，圓外一點P到圓心O的距離為2，過P引圓O的兩條切線，切點分別記為A、B，M為圓O上的一個動點，則
PA
?
PM
的最小值為（　　）

6．已知雙曲線C：
x
2
12
-
y
2
4
=1，點F是C的右焦點，若點P為C左支上的動點，設點P到C的一條漸近線的距離為d,則d+|PF|的最小值為（　　）

7．如圖1所示，四邊形ABCD是邊長為2的正方形，點E、F、M分別為線段BC、CD、BE的中點，分別沿AE、AF及EF所在直線把△AEB，△AFD和△EFC折起，使B、C、D三點重合于點P，得到如圖2所示的三棱錐P-AEF，則下列結論中正確的有（　　）

22．已知函數f（x）=e^x+2ax-1，其中a為實數，e為自然對數底數，e=2.71828?．
（1）已知函數x∈R，f（x）≥0，求實數a取值的集合；
（2）已知函數F（x）=f（x）-ax²有兩個不同極值點x₁、x₂，證明
2
a
（
x
1
+
x
2
）
＞
3
x
1
x
2
．