2022-2023學年湖北省襄陽市樊城區(qū)高一（上）月考數學試卷

一、單選題

• 1．已知集合A={x|x²-5x+6≤0}，集合

  B

  =

  {

  x

  |

  y

  =

  lo

  g

  2

  （

  x

  -

  1

  ）

  }

  ，則A∪B=（　　）

  A．（1，3]

  B．（1，+∞）

  C．[2，+∞）

  D．[2，3]
  組卷：4引用：4難度：0.8

  解析

• 2．下列說法正確的是（　　）

  A．第二象限角比第一象限角大

  B．60°角與600°角是終邊相同角

  C．三角形的內角是第一象限角或第二象限角

  D．將表的分針撥慢10分鐘，則分針轉過的角的弧度數為 π 3
  組卷：737引用：17難度：0.9

  解析

• 3．命題“?x∈R，2kx²+kx-

  3

  8

  ＜0”為真命題的一個充分不必要條件是（　　）

  A．（-3，0）

  B．（-3，0]

  C．（-3，1）

  D．（-3，+∞）
  組卷：360引用：9難度：0.7

  解析

• 4．設a=log₃2，b=log₆4，c=log_3e（2e），則（　　）

  A．c＜b＜a

  B．a＜b＜c

  C．b＜a＜c

  D．a＜c＜b
  組卷：458引用：4難度：0.5

  解析

• 5．我國著名數學家華羅庚曾說過：“數無形時少直觀，形無數時難入微；數形結合百般好，隔離分家萬事休”．函數f（x）=

  x

  2

  +

  4

  x

  +

  1

  x

  2

  +

  1

  的部分圖象大致是（　　）

  A．

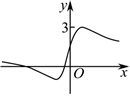
  B．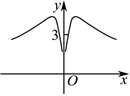

  C．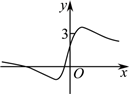

  D．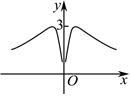
  組卷：209引用：10難度：0.7

  解析

• 6．已知函數f（x）=

  2

  x

  -

  1

  2

  x

  +

  1

  +ax²⁰²³-

  b

  x

  -6，f（-2）=5，則f（2）=（　　）

  A．12

  B．-12

  C．-17

  D．17
  組卷：67引用：3難度：0.7

  解析

• 7．某大型民企為激勵創(chuàng)新，計劃逐年加大研發(fā)資金投入．若該民企2021年全年投入研發(fā)資金130萬元，在此基礎上，每年投入的研發(fā)資金比上一年增長12%，則該民企全年投入的研發(fā)資金開始超過200萬元的年份是（參考數據：lg1.12≈0.05，lg1.3≈0.11，lg2≈0.30）（　　）

  A．2022年

  B．2023年

  C．2024年

  D．2025年
  組卷：6引用：2難度：0.7

  解析

四、解答題

• 21．已知定義域為R的函數f（x）=

  b

  x

  +

  n

  -

  2

  b

  x

  -

  2

  是奇函數，且指數函數y=b^x的圖象過點（2，4）．
  （1）求f（x）的表達式；
  （2）若方程f（x²+3x）+f（-a+x）=0，x∈（-4，+∞）恰有2個互異的實數根，求實數a的取值集合；
  （3）若對任意的t∈[-1，1]，不等式f（t²-2a）+f（at-1）≥0恒成立，求實數a的取值范圍．
  組卷：56引用：4難度：0.5

  解析

• 22．已知a∈R，當x＞0時，f（x）=log₂（

  1

  x

  +

  a

  ）．
  （Ⅰ）若函數f（x）過點（1，1），求此時函數f（x）的解析式；
  （Ⅱ）若函數g（x）=f（x）+2log₂x只有一個零點，求實數a的值；
  （Ⅲ）設a＞0，若對任意實數t∈[

  1

  3

  ，1]，函數f（x）在[t,t+1]上的最大值與最小值的差不大于1，求實數a的取值范圍．
  組卷：16引用：2難度：0.5

  解析