2021-2022學年海南省屯昌中學高一（下）期中數學試卷

一、單選題

• 1．已知某圓錐的母線長為3，底面圓的半徑為2．則圓錐的表面積為（　　）

  A．10π

  B．12π

  C．14π

  D．16π
  組卷：26引用：2難度：0.6

  解析

• 2．若復數z滿足（2+i）z=1+i（其中i為虛數單位），則z的共軛復數在復平面內對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：94引用：8難度：0.8

  解析

• 3．△ABC的三個內角A、B、C滿足sinA：sinB：sinC=2：3：4，則cosA=（　　）

  A． 2 9

  B． 7 8

  C． 15 8

  D． 15 4
  組卷：31引用：1難度：0.7

  解析

• 4．已知函數

  f

  （

  x

  ）

  =

  cos

  （

  2

  x

  -

  π

  3

  ）

  ，先將其圖象上的所有點的橫坐標伸長到原來的4倍（縱坐標不變），再將所得到的圖象向右平移

  2

  π

  3

  個單位長度，得到函數g（x）的圖象，則（　　）

  A．g（x）的最小正周期是2π

  B．g（x）的最小值為-2

  C．g（x）在（0，π）上單調遞增

  D．g（x）的圖象關于點 （ π 2 ， 0 ） 對稱
  組卷：179引用：4難度：0.5

  解析

• 5．在古希臘數學家海倫的著作《測地術》中記載了著名的海倫公式，利用三角形的三邊長求三角形的面積．若三角形的三邊分別為a,b,c?，則其面積

  S

  =

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  ?，這里

  p

  =

  a

  +

  b

  +

  c

  2

  ?．已知在△ABC?中，內角A，B，C?所對的邊分別為a,b,c,a=6，b+c=10?，則△ABC?的面積最大值為（　　）

  A． 6 3 ?

  B． 8 2 ?

  C．10?

  D．12?
  組卷：62引用：2難度：0.7

  解析

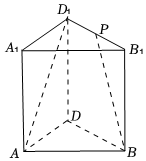• 6．如圖，在直三棱柱ABD-A₁B₁D₁中，AB=AD=AA₁，∠ABD=45°，P為B₁D₁的中點，則直線PB與AD₁所成的角為（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：758引用：10難度：0.6

  解析

• 7．正四面體內放入一個可以自動充氣的球，當球和四面體的面相切時，球的半徑與該正四面體的高的比值為（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 1 5
  組卷：207引用：5難度：0.6

  解析

四、解答題

• 21．如圖，已知直三棱柱ABC-A₁B₁C₁，AB⊥AC，AB=2，AC=4，AA₁=2，E，F是A₁B₁和A₁C₁上的兩點，且A₁E=1，

  EF

  =

  5

  ．
  （1）證明：B，C，E，F四點共面；
  （2）求點A到平面BCE的距離．
  組卷：12引用：1難度：0.5

  解析

• 22．重慶是我國著名的“火爐”城市之一，如圖，重慶某避暑山莊O為吸引游客，準備在門前兩條小路OA和OB之間修建一處弓形花園，使之有著類似“冰淇淋”般的涼爽感，已知∠AOB=

  π

  6

  ，弓形花園的弦長|AB|=2

  3

  ，記弓形花園的頂點為M，∠MAB=∠MBA=

  π

  6

  ，設∠OBA=θ．
  
  （Ⅰ）將|OA|，|OB|用含有θ的關系式表示出來；
  （Ⅱ）該山莊準備在M點處修建噴泉，為獲取更好的觀景視野，如何設計OA、OB的長度，才使得噴泉M與山莊O的距離的值最大？
  組卷：229引用：10難度：0.5

  解析