2023年海南省五指山市中考數學一模試卷

一、選擇題（本大題共12小題，每小題3分，共36分．在每小題給出的四個選項中，只有一個選項是符合題目要求的）

• 1．下列各數中，3的相反數的倒數是（　　）

  A．3

  B．-3

  C． 1 3

  D． - 1 3
  組卷：108引用：7難度：0.8

  解析

• 2．光刻機采用類似照片沖印的技術，把掩膜版上的精細圖形通過光線的曝光印制到硅片上，是制造芯片的核心裝備．ArF準分子激光是光刻機常用光源之一，其波長為0.000000193米，該光源波長用科學記數法表示為（　　）

  A．193×106米	B．193×10-9米
  C．1.93×10-7米	D．1.93×10-9米
  組卷：284引用：9難度：0.8

  解析

• 3．如圖是一個由5個相同的正方體組成的立體圖形，它的左視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：221引用：7難度：0.9

  解析

• 4．關于x的一元一次不等式

  1

  -

  x

  3

  +2≤

  x

  +

  1

  2

  的解集為（　　）

  A．x≤ 1 5

  B．x≥ 1 5

  C．x≤ 11 5

  D．x≥ 11 5
  組卷：610引用：6難度：0.9

  解析

• 5．如圖，AB∥CD，∠1=70°，則∠2=（　　）

  A．70°

  B．80°

  C．110°

  D．120°
  組卷：344引用：17難度：0.9

  解析

• 6．小明用計步器記錄自己一個月（30天）每天走的步數，并繪制成如下統計表：
  

  步數（萬步）	1.0	1.1	1.2	1.3	1.4
  天數	3	3	9	11	4

  在每天所走的步數這組數據中，眾數和中位數分別是（　　）

  A．1.3，1.25

  B．1.3，1.3

  C．1.4，1.3

  D．1.3，1.1
  組卷：165引用：5難度：0.7

  解析

• 7．分式方程

  5

  x

  -

  2

  =

  3

  x

  的解是（　　）

  A．x=3

  B．x=-3

  C．x=-1

  D．x=1
  組卷：384引用：7難度：0.8

  解析

三、（本大題共6小題，17題12分，18、19、20題各10分，21、22題15分，本大題滿分72分）

• 21．（1）閱讀理解：如圖1，在△ABC中，若AB=3，AC=5．求BC邊上的中線AD的取值范圍，小聰同學是這樣思考的：延長AD至E，使DE=AD，連接BE．利用全等將邊AC轉化到BE，在△BAE中利用三角形三邊關系即可求出中線AD的取值范圍，在這個過程中小聰同學證三角形全等用到的判定方法是

  ，中線AD的取值范圍是

  ；
  （2）問題解決：如圖2，在△ABC中，點D是BC的中點，DM⊥DN．DM交AB于點M，DN交AC于點N．求證：BM+CN＞MN；
  （3）問題拓展：如圖3，在△ABC中，點D是BC的中點，分別以AB，AC為直角邊向△ABC外作Rt△ABM和Rt△ACN，其中∠BAM=∠NAC=90°，AB=AM，AC=AN，連接MN，請你探索AD與MN的數量與位置關系，并直接寫出AD與MN的關系．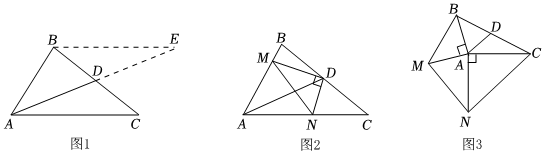
  
  組卷：368引用：20難度：0.1

  解析

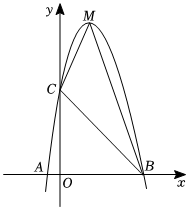• 22．如圖，二次函數y=ax²+bx+5的圖象經過點（1，8），且與x軸交于A、B兩點，與y軸交于點C，其中點A（-1，0），M為拋物線的頂點．
  （1）求二次函數的解析式；
  （2）求△MCB的面積；
  （3）在坐標軸上是否存在點N，使得△BCN為直角三角形？若存在，求出點N的坐標；若不存在，請說明理由．
  組卷：1429引用：7難度：0.5

  解析