2023-2024學年浙江省臺州市溫嶺中學高一（上）月考數學試卷

一、單選題（本題共6小題，每題5分，共30分）

• 1．已知集合M={-2，-1，0，1，2}，N={x|x²-x-6≥0}，則M∩N=（　　）

  A．{-2，-1，0，1}

  B．{0，1，2}

  C．{-2}

  D．{2}
  組卷：5107引用：57難度：0.9

  解析

• 2．已知命題p：“?x∈R，x²-ax+1＜0”為假命題，則實數a的取值范圍為（　　）

  A．（-∞，2]	B．（-2，2）
  C．（-∞，-2）∪（2，+∞）	D．[-2，2]
  組卷：278引用：7難度：0.9

  解析

• 3．函數f（x）=

  m

  x

  2

  -

  2

  x

  +

  1

  的定義域為R，則實數m的取值范圍是（　　）

  A．（0，1）

  B．（1，+∞）

  C．[1，+∞）

  D．[0，+∞）
  組卷：44引用：6難度：0.9

  解析

• 4．下列選項中表示同一函數的是（　　）

  A．f（x）=x0與g（x）=1

  B．f（x）=x與 g （ x ） = x 2 x

  C． f （ x ） = （ x - 1 ） 2 與g（x）=x-1

  D． f （ x ） = 1 ， x ≥ 0 - 1 ， x ＜ 0 與 g （ x ） = x | x | ， x ≠ 0 1 ， x = 0
  組卷：107引用：14難度：0.8

  解析

• 5．已知不等式a（x-x₁）（x-x₂）＞0的解集為A，不等式b（x-x₁）（x-x₂）≥0的解集為B，其中a、b都是非零常數，則“ab＜0”是“A∪B=R”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既非充分也非必要條件
  組卷：142引用：11難度：0.7

  解析

四、解答題（本題共4小題，共40分。解答應寫出文字說明、證明過程或演算步驟）

• 15．已知函數

  f

  （

  x

  ）

  =

  2

  x

  +

  b

  x

  +

  a

  ，x∈[-1，1]，滿足條件

  f

  （

  0

  ）

  =

  5

  2

  ，f（-1）=3．
  （1）求f（x）的解析式；
  （2）用單調性的定義證明f（x）在x∈[-1，1]上的單調性，并求f（x）在x∈[-1，1]上的最值．
  組卷：110引用：6難度：0.6

  解析

• 16．如圖，在平面直角坐標系中，直線

  y

  =

  1

  2

  x

  +

  2

  與x軸交于點A，與y軸交于點C，二次函數

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  的圖象經過A、C兩點，與x軸的另一交點為點B．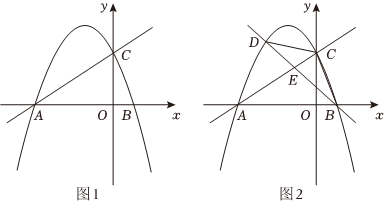
  
  （1）求二次函數的表達式；
  （2）當m≤x≤m+1時，二次函數

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  的最大值為-2m,求m的值；
  （3）如圖2，點D為直線AC上方二次函數圖象上一動點，連接BC、CD，設直線BD交線段AC于點E，△CDE面積為S₁，△BCE的面積為S₂，求

  S

  1

  S

  2

  的最大值．
  組卷：27引用：2難度：0.4

  解析