當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省茂名一中高一（上）期中數學試卷

發布：2024/10/4 0:0:1

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．若扇形的周長為12cm,面積為8cm²，則其圓心角的弧度數是（　　）
A．1或4 B．1或2 C．2或4 D．1或5
組卷：405引用：6難度：0.7
解析
2．已知函數y=log_a（x+2）+3的圖象恒過定點A，若角α的頂點與原點重合，始邊與x軸的非負半軸重合，且點A在角α的終邊上，則sinα的值為（　　）
A．
-
17
17
B．
4
17
17
C．
3
10
10
D．
-
10
10
組卷：71引用：2難度：0.8
解析
3．tan（α+β）=
2
5
，tan（α-β）=
1
4
，則tan2α=（　　）
A．
1
6
B．
22
13
C．
3
22
D．
13
18
組卷：88引用：8難度：0.9
解析
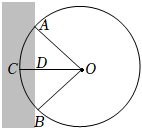4．我國古代數學經典著作《九章算術》中記載了一個“圓材埋壁”的問題：“今有圓材埋在壁中，不知大小，以鋸鋸之，深一寸，鋸道長一尺，問徑幾何？”現有一類似問題，不確定大小的圓柱形木材，部分埋在墻壁中，其截面如圖所示．用鋸去鋸這木材，若鋸口深
CD
=
2
-
3
，鋸道AB=2，則圖中
?
ACB
與弦AB圍成的弓形的面積為（　　）
A．
π
2
-
3
2
B．
2
π
3
-
3
C．
π
3
-
3
2
D．
π
3
-
3
3
組卷：275引用：11難度：0.7
解析
5．函數y=
sinx
+
4
x
e
|
x
|
的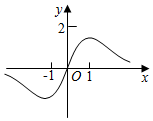圖象大致為（　　）
A． B．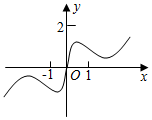
C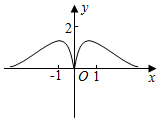． D．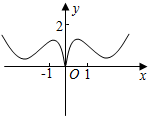
組卷：467引用：14難度：0.7
解析
6．已知α為第二象限角，則
cosα
1
+
sinα
1
-
sinα
+
si
n
2
α
1
+
1
tan
2
α
=（　　）
A．1 B．-1 C．0 D．2
組卷：217引用：4難度：0.8
解析
7．設a=
3
2
cos
6
°
-
1
2
sin
6
°
，b=
2
tan
27
°
1
-
tan
2
27
°
，c=
1
-
cos
110
°
2
，則有（　　）
A．c＜b＜a B．a＜b＜c C．a＜c＜b D．b＜c＜a
組卷：236引用：3難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分，其中第17題10分，第18-22題每題12分．解答應寫出必要的文字說明、證明過程或演算步驟．

21．已知函數
f
（
x
）
=
sin
2
x
+
3
cos
2
x
．
（Ⅰ）若函數y=f（x+m）是偶函數，求|m|的最小值；
（Ⅱ）若
f
（
α
2
）
=
8
5
，
α
∈
（
0
，
π
2
）
，求cosα的值；
（Ⅲ）求函數F（x）=[f（x）]²-n?f（x）+1在
x
∈
[
-
π
4
，
π
6
]
上的最大值．
組卷：200引用：4難度：0.4
解析
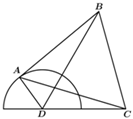22．為提升城市旅游景觀面貌，城建部門擬對一公園進行改造，已知原公園是直徑為2百米的半圓，出入口在圓心D處，C點為一居民小區，CD距離為2百米，按照設計要求，取圓弧上一點A，并以線段AC為一邊向圓外作等邊三角形ABC，使改造之后的公園成四邊形ABCD，并將△BCD區域建成免費開放的植物園，如圖所示．設∠ADC=θ．
（1）當
θ
=
5
π
6
，求四邊形ABCD的面積；
（2）當θ為何值時，線段BD最長并求最長值．
組卷：31引用：4難度：0.6
解析