2022年陜西省西安市高考數學第二次質檢試卷（文科）

一、選擇題：本題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．設集合U={0，1，3，5，6，8}，A={1，5，8}，B={2}，則（?_UA）∪B=（　　）

  A．{0，2，3，6}

  B．{0，3，6}

  C．{1，2，5，8}

  D．?
  組卷：194引用：6難度：0.9

  解析

• 2．計算：

  2

  -

  3

  i

  1

  -

  i

  =（　　）

  A． 5 2 + i 2

  B． 5 2 - i 2

  C． - 5 2 + i 2

  D． - 5 2 - i 2
  組卷：114引用：2難度：0.9

  解析

• 3．已知a,b都是實數，則“

  lo

  g

  2

  1

  a

  ＜

  lo

  g

  2

  1

  b

  ”是“a＞b＞0”的（　　）

  A．充要條件	B．必要不充分條件
  C．充分不必要條件	D．既不充分也不必要條件
  組卷：94引用：1難度：0.7

  解析

• 4．已知雙曲線

  C

  ：

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =1（a＞0，b＞0）的一條漸近線與x軸正半軸所成夾角為

  π

  3

  ，則C的離心率為（　　）

  A． 2 3 3

  B．2

  C． 3

  D．3
  組卷：140引用：2難度：0.7

  解析

• 5．若函數f（x+1）為偶函數，對任意x₁，x₂∈[1，+∞）且x₁≠x₂，都有（x₂-x₁）[f（x₁）-f（x₂）]＞0，則有（　　）

  A． f （ 1 3 ） ＜ f （ 3 2 ） ＜ f （ 2 3 ）	B． f （ 2 3 ） ＜ f （ 3 2 ） ＜ f （ 1 3 ）
  C． f （ 2 3 ） ＜ f （ 1 3 ） ＜ f （ 3 2 ）	D． f （ 3 2 ） ＜ f （ 2 3 ） ＜ f （ 1 3 ）
  組卷：911引用：5難度：0.7

  解析

• 6．如果函數y=3cos（2x+φ）的圖象關于點（

  4

  π

  3

  ，0）中心對稱，那么|φ|的最小值為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 2
  組卷：2789引用：86難度：0.9

  解析

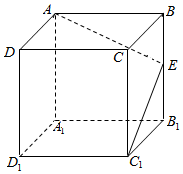• 7．如圖，點E為正方體ABCD-A₁B₁C₁D₁的棱BB₁的中點，用過點A，E，C₁的平面截去該正方體的上半部分，則剩余幾何體的側視圖為（　　）

  A．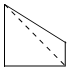

  B．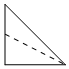

  C．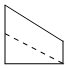

  D．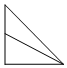
  組卷：204引用：3難度：0.9

  解析

（二）選考題：共10分.請考生在第22、23題中任選一題作答.如果多做，則按所做的第一題計分.[選修4-4：坐標系與參數方程]

• 22．在平面直角坐標系xOy中，直線l的參數方程為

  x = 1 + tcosα

  y = tsinα

  （t為參數），以O為極點，x軸正半軸為極軸建立極坐標系，曲線C的極坐標方程為

  ρ

  2

  =

  12

  4

  -

  cos

  2

  θ

  ．
  （1）求曲線C的直角坐標方程；
  （2）設直線l與曲線C交于A，B兩點，點D是AB的中點，點F（1，0），求|DF|的取值范圍．
  組卷：197引用：3難度：0.7

  解析

[選修4-5：不等式選講]

• 23．設不等式|2x-1|＜1的解集是M，且a,b∈M．
  （1）試比較ab+1與a+b的大小；
  （2）設maxA表示數集A中的最大數，

  h

  =

  max

  {

  1

  ab

  ，

  a

  2

  +

  b

  2

  ab

  }

  ，證明：

  h

  ≥

  2

  ．
  組卷：41引用：3難度：0.5

  解析