2022-2023學(xué)年河南省南陽市高一（上）期末數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

• 1．函數(shù)g（x）=log₃（x+1）的定義域?yàn)锳，不等式

  x

  +

  2

  x

  -

  1

  ≤0的解集為B，則A∩B=（　　）

  A．（-1，1）

  B．[-2，-1）

  C．[-1，1）

  D．[-2，1）
  組卷：64引用：2難度：0.7

  解析

• 2．我市某所高中每天至少用一個(gè)小時(shí)學(xué)習(xí)數(shù)學(xué)的學(xué)生共有1200人，其中一、二、三年級(jí)的人數(shù)比為3：4：5，要用分層隨機(jī)抽樣的方法從中抽取一個(gè)容量為120的樣本，則應(yīng)抽取的一年級(jí)學(xué)生的人數(shù)為（　　）

  A．20

  B．30

  C．40

  D．50
  組卷：135引用：2難度：0.8

  解析

• 3．三個(gè)實(shí)數(shù)a=log₃4，b=log₂5，c=3

  -

  1

  2

  的大小關(guān)系為（　　）

  A．a(chǎn)＜c＜b

  B．c＜a＜b

  C．c＜b＜a

  D．b＜c＜a
  組卷：71引用：4難度：0.7

  解析

• 4．總體由編號(hào)為01，02，…，20的20個(gè)個(gè)體組成，用下面的隨機(jī)數(shù)表選取6個(gè)個(gè)體，選取方法是從隨機(jī)數(shù)表第1行的第9列的數(shù)字開始由左到右依次選取兩個(gè)數(shù)字，則選出來的第6個(gè)個(gè)體的編號(hào)為（　　）
  7816  6572  0802  6314  0219  4308  9714  0198
  3208  9216  4936  8200  3623  4869  6938  7181

  A．08

  B．14

  C．16

  D．19
  組卷：99引用：1難度：0.7

  解析

• 5．Logistic模型是常用數(shù)學(xué)模型之一，可用于流行病學(xué)領(lǐng)域．有學(xué)者根據(jù)所公布的數(shù)據(jù)建立了某地區(qū)新冠肺炎累計(jì)確診病例I（t）（t的單位：天）的Logistic模型：

  I

  （

  t

  ）

  =

  K

  1

  +

  e

  12

  -

  t

  4

  ，其中K為最大確診病例數(shù)．當(dāng)I（t₀）=0.05K時(shí)，標(biāo)志著已初步遏制疫情，則t₀約為（　　）（ln19≈3）

  A．35

  B．36

  C．60

  D．40
  組卷：204引用：3難度：0.6

  解析

• 6．已知f（x+1）是定義在R上的偶函數(shù)，且對(duì)任意的1≤x₁＜x₂，都有（x₁-x₂）[f（x₁）-f（x₂）]＜0恒成立，則關(guān)于x的不等式f（2x）＞f（x-1）的解集為（　　）

  A．（-∞，-1）	B．（-1，+∞）
  C．（-1，1）	D．（-∞，-1）∪（1，+∞）
  組卷：106引用：1難度：0.6

  解析

• 7．甲、乙、丙三人打靶，他們的命中率分別為p₁，p₂，

  1

  3

  ，若三人同時(shí)射擊一個(gè)目標(biāo)，甲、丙擊中目標(biāo)而乙沒有擊中目標(biāo)的概率為

  1

  18

  ，乙擊中目標(biāo)而丙沒有擊中目標(biāo)的概率為

  4

  9

  ．已知“甲擊中目標(biāo)”，“乙擊中目標(biāo)”，“丙擊中目標(biāo)”是相互獨(dú)立事件，則p₁，p₂的值分別為（　　）

  A．p1= 1 3 ，p2= 1 2	B．p1= 1 3 ，p2= 2 3
  C．p1= 1 2 ，p2= 2 3	D．p1= 2 3 ，p2= 1 2
  組卷：180引用：3難度：0.8

  解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。

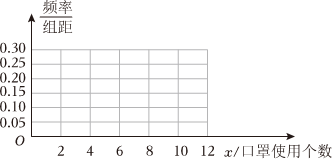• 21．2022年入冬以來，為進(jìn)一步做好疫情防控工作，避免疫情的再度爆發(fā)，A地區(qū)規(guī)定居民出行或者出席公共場(chǎng)合均需佩戴口罩，現(xiàn)將A地區(qū)20000個(gè)居民一周的口罩使用個(gè)數(shù)統(tǒng)計(jì)如表所示，其中每周的口罩使用個(gè)數(shù)在6以上（含6）的有14000人．
  

  口罩使用數(shù)量	[2，4）	[4，6）	[6，8）	[8，10）	[10，12]
  頻率	0.2	m	0.3	n	0.1

  （1）求m,n的值，根據(jù)表中數(shù)據(jù)，完善上面的頻率分布直方圖；（只畫圖，不要過程）
  （2）根據(jù)頻率分布直方圖估計(jì)A地區(qū)居民一周口罩使用個(gè)數(shù)的75%分位數(shù)和中位數(shù)；（四舍五入，精確到0.1）
  （3）根據(jù)頻率分布直方圖估計(jì)A地區(qū)居民一周口罩使用個(gè)數(shù)的平均數(shù)以及方差．（每組數(shù)據(jù)用每組中點(diǎn)值代替）
  組卷：110引用：3難度：0.7

  解析

• 22．已知函數(shù)f（x）=kx-log₂（2^x+1）（k∈R）的圖像關(guān)于y軸對(duì)稱．
  （1）求k的值；
  （2）若函數(shù)g（x）=2

  1

  2

  x

  -

  f

  （

  x

  ）

  -m?2^1+kx-1，x∈[0，log₂9]，m∈R，求g（x）的最大值g（m）．
  組卷：66引用：1難度：0.5

  解析