當前位置：試卷中心 > 試卷詳情

2021-2022學年內蒙古赤峰市紅旗中學高一（上）期末數學試卷（理科）

發布：2024/4/20 14:35:0

一、選擇題：本大題共12小題，每小題5分，在每小題給出的四個選項中，只有一項是符合題目要求的.

1．方程x²=2x的所有實數根組成的集合為（　　）
A．（0，2） B．{（0，2）} C．{0，2} D．{x²=2x}
組卷：19引用：2難度：0.7
解析
2．下列各角中，與60°角終邊相同的角是（　　）
A．-300° B．-60° C．600° D．1380°
組卷：797引用：9難度：0.9
解析
3．函數
f
（
x
）
=
4
-
x
x
-
1
的定義域為（　　）
A．（-∞，4） B．[4，+∞）
C．（-∞，4] D．（-∞，1）∪（1，4]
組卷：193引用：6難度：0.9
解析
4．函數
y
=
cos
（
2
πx
+
π
6
）
的最小正周期是（　　）
A．1 B．2 C．π D．2π
組卷：92引用：4難度：0.7
解析
5．納皮爾是蘇格蘭數學家，其主要成果有球面三角中納皮爾比擬式、納皮爾圓部法則（1614）和納皮爾算籌（1617），而最大的貢獻是對數的發明，著有《奇妙的對數定律說明書》，并且發明了對數尺，可以利用對數尺查詢出任意一對數值．現將物體放在空氣中冷卻，如果物體原來的溫度是T₁（°C），空氣的溫度是T₀（°C），經過t分鐘后物體的溫度T（°C）可由公式
t
=
4
lo
g
3
T
1
-
T
0
T
-
T
0
得出，如溫度為90°C的物體，放在空氣中冷卻2.5236分鐘后，物體的溫度是50℃，若根據對數尺可以查詢出log₃2=0.6309，則空氣溫度是（　　）
A．5°C B．10°C C．15°C D．20°C
組卷：63引用：6難度：0.8
解析
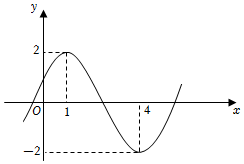6．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜
π
2
）的圖象如圖，若x₁，x₂∈（1，4），且f（x₁）+f（x₂）=0（x₁≠x₂），則
f
（
x
1
+
x
2
2
）
=（　　）
A．1 B．0 C．
1
2
D．
-
1
2
組卷：161引用：3難度：0.7
解析
7．已知實數a滿足3^a=5，則函數f（x）=a^x+2x-log₅3的零點在下列哪個區間內（　　）
A．（-2，-1） B．（-1，0） C．（0，1） D．（1，2）
組卷：72引用：3難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

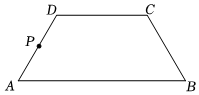21．如圖，在等腰梯形ABCD中，
|
AB
|
=
2
|
DC
|
=
4
，
∠
DAB
=
π
4
．
（1）若
k
AB
-
AD
與
AC
共線，求k的值；
（2）若P為AD邊上的動點，求
（
PA
+
PB
）
?
PC
的最大值．
組卷：269引用：2難度：0.6
解析
22．在①函數
f
（
x
）
=
1
2
sin
（
2
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
的圖象向右平移
π
12
個單位長度得到g（x）的圖象，且g（x）圖象關于原點對稱；
②向量
m
=
（
3
sinωx
,
cos
2
ωx
）
，
n
=
（
1
2
cosωx
,
1
4
）
，ω＞0，
f
（
x
）
=
m
?
n
；
③函數
f
（
x
）
=
cosωxsin
（
ωx
+
π
6
）
-
1
4
（
ω
＞
0
）
．在以上三個條件中任選一個，補充在下面問題中空格位置，并解答．
已知_____，函數f（x）的圖象相鄰兩條對稱軸之間的距離為
π
2
．
（1）若
0
＜
θ
＜
π
2
，且
sinθ
=
2
2
，求f（θ）的值；
（2）求函數f（x）在[0，2π]上的單調遞減區間．
組卷：72引用：2難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（-∞，4）	B．[4，+∞）
C．（-∞，4]	D．（-∞，1）∪（1，4]

2021-2022學年內蒙古赤峰市紅旗中學高一（上）期末數學試卷（理科）

一、選擇題：本大題共12小題，每小題5分，在每小題給出的四個選項中，只有一項是符合題目要求的.

1．方程x2=2x的所有實數根組成的集合為（ ）

2．下列各角中，與60°角終邊相同的角是（ ）

3．函數f（x）=4-xx-1的定義域為（ ）

4．函數y=cos（2πx+π6）的最小正周期是（ ）

6．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π2）的圖象如圖，若x1，x2∈（1，4），且f（x1）+f（x2）=0（x1≠x2），則f（x1+x22）=（ ）

7．已知實數a滿足3a=5，則函數f（x）=ax+2x-log53的零點在下列哪個區間內（ ）

三、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

21．如圖，在等腰梯形ABCD中，|AB|=2|DC|=4，∠DAB=π4．（1）若kAB-AD與AC共線，求k的值；（2）若P為AD邊上的動點，求（PA+PB）?PC的最大值．

1．方程x²=2x的所有實數根組成的集合為（　　）

2．下列各角中，與60°角終邊相同的角是（　　）

3．函數
f
（
x
）
=
4
-
x
x
-
1
的定義域為（　　）

4．函數
y
=
cos
（
2
πx
+
π
6
）
的最小正周期是（　　）

6．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜
π
2
）的圖象如圖，若x₁，x₂∈（1，4），且f（x₁）+f（x₂）=0（x₁≠x₂），則
f
（
x
1
+
x
2
2
）
=（　　）

7．已知實數a滿足3^a=5，則函數f（x）=a^x+2x-log₅3的零點在下列哪個區間內（　　）

21．如圖，在等腰梯形ABCD中，
|
AB
|
=
2
|
DC
|
=
4
，
∠
DAB
=
π
4
．
（1）若
k
AB
-
AD
與
AC
共線，求k的值；
（2）若P為AD邊上的動點，求
（
PA
+
PB
）
?
PC
的最大值．