2023年安徽省滁州市定遠縣義和中學中考數學一模試卷

一、選擇題（本大題共10小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．在-（-5），-|-3|，4，-4這4個數中，最小的有理數是（　　）

  A．-（-5）

  B．-|-3|

  C．4

  D．-4
  組卷：80引用：3難度：0.7

  解析

• 2．下列運算正確的是（　　）

  A．a2?a3=a6	B．2a2÷a=2
  C．a2+2a2=3a2	D．（x-y）2=x2-y2
  組卷：28引用：2難度：0.8

  解析

• 3．據中國鐵路3月1日發布的新聞稿知，2021年鐵路春運圓滿結束，全國鐵路累計發送旅客413300000人次，數413300000用科學記數法記為（　　）

  A．4133×108

  B．4133×105

  C．4.133×108

  D．4.133×105
  組卷：8引用：2難度：0.7

  解析

• 4．如圖需再添上一個面，折疊后才能圍成一個正方體，下面是四位同學補畫的情況（圖中陰影部分），其中正確的是（　　）

  A．

  B．

  C．

  D．
  組卷：56引用：9難度：0.9

  解析

• 5．已知關于x、y的二元一次方程ax+b=y,下表列出了當x分別取值時對應的y值．則關于x的不等式ax+b＜0的解集為（　　）
  

  x	…	-2	-1	0	1	2	3	…
  y	…	3	2	1	0	-1	-2	…

  A．x＜1

  B．x＞1

  C．x＜0

  D．x＞0
  組卷：909引用：9難度：0.8

  解析

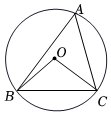• 6．如圖，⊙O是△ABC的外接圓，∠OCB=40°，則∠A的度數是（　　）

  A．40°

  B．80°

  C．50°

  D．45°
  組卷：341引用：4難度：0.7

  解析

• 7．在一次舞蹈比賽中，甲、乙、丙、丁四隊女演員的人數相同，身高的平均數均為166cm,且方差分別為

  s

  2

  甲

  =3.1，s²_乙=2.9，s²_丙=2.3，s²_丁=1.8，則這四隊女演員的身高最整齊的是（　　）

  A．甲隊

  B．乙隊

  C．丙隊

  D．丁隊
  組卷：82引用：6難度：0.7

  解析

三、解答題（本大題共9小題，共90分。解答應寫出文字說明，證明過程或演算步驟）

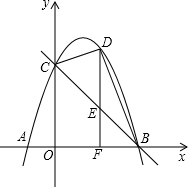• 22．如圖，已知拋物線y=-x²+bx+c與x軸交于A、B兩點，與y軸交于點C，且點A的坐標為（-1，0），直線y=kx+3經過點B、C．
  （1）拋物線解析式為

  ，直線BC解析式為

  ；
  （2）點D是第一象限內拋物線上的一個動點（與點C，B不重合），過點D作DF⊥x軸于點F，交直線BC于點E，連接BD，CD．設點D的橫坐標為m,△BCD的面積為S，求S關于m的函數解析式及自變量m的取值范圍，并求出S的最大值；
  （3）已知點M為拋物線對稱軸上的一個動點，若△MBC是以BC為直角邊的直角三角形，請直接寫出點M的坐標．
  組卷：305引用：4難度：0.4

  解析

• 23．定義：我們知道，四邊形的一條對角線把這個四邊形分成了兩個三角形，如果這兩個三角形相似（不全等），我們就把這條對角線叫做這個四邊形的“相似對角線”．
  （1）如圖1，△ABC的三個頂點均在正方形網格中的格點上，若四邊形ABCD是以AC為“相似對角線”的四邊形，請只用無刻度的直尺，就可以在網格中畫出點D，請你在圖1中找出滿足條件的點D，保留畫圖痕跡（找出2個即可）
  （2）①如圖2，在四邊形ABCD中，∠DAB=90°，∠DCB=135°，對角線AC平分∠DAB．請問AC是四邊形ABCD的“相似對角線”嗎？請說明理由；
  ②若AC=

  10

  ，求AD?AB的值．
  （3）如圖3，在（2）的條件下，若∠D=∠ACB=90°時，將△ADC以A為位似中心，位似比為

  5

  ：

  2

  縮小得到△AEF，連接CE、BF，在△AEF繞點A旋轉的過程中，當CE所在的直線垂直于AF時，請你直接寫出BF的長．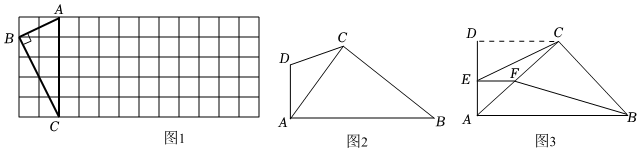
  
  組卷：918引用：4難度：0.3

  解析