2022-2023學(xué)年河南師大附中等十校聯(lián)考九年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題（下列各題中，只有一個(gè)選項(xiàng)是符合題目要求的，請(qǐng)?jiān)诖痤}卡上指定的位置填涂符合要求的選項(xiàng)前面的字母代號(hào)．每題3分，計(jì)33分．）

• 1．我國古代《九章算術(shù)》中注有“今兩算得失相反，要令正負(fù)以名之”意思是今有兩數(shù)其意義相反，則分別叫做正數(shù)與負(fù)數(shù)．如果向北走兩步記作+2步，那么向南走5步記作（　　）

  A．+5步

  B．-5步

  C．-3步

  D．-2步
  組卷：901引用：8難度：0.9

  解析

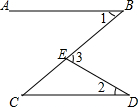• 2．如圖，AB∥CD，點(diǎn)E在線段BC上，若∠1=40°，∠2=30°，則∠3的度數(shù)是（　　）

  A．70°

  B．60°

  C．55°

  D．50°
  組卷：149引用：87難度：0.9

  解析

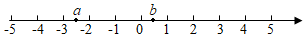• 3．實(shí)數(shù)a,b在數(shù)軸上的對(duì)應(yīng)點(diǎn)的位置如圖所示，下列結(jié)論中正確的是（　　）

  A．a(chǎn)＞-2

  B．|a|＞b

  C．a(chǎn)+b＞0

  D．b-a＜0
  組卷：2297引用：18難度：0.7

  解析

• 4．若分式

  |

  x

  |

  -

  1

  x

  -

  1

  的值等于0，則x的值為（　　）

  A．-1

  B．0

  C．1

  D．±1
  組卷：2055引用：13難度：0.9

  解析

• 5．下列計(jì)算正確的是（　　）

  A．a(chǎn)2?a4=a8	B．（-2a2）3=-6a6
  C．a(chǎn)4÷a=a3	D．2a+3a=5a2
  組卷：448引用：14難度：0.9

  解析

• 6．某地開展建設(shè)綠色家園活動(dòng)，活動(dòng)期間，計(jì)劃每天種植相同數(shù)量的樹木．該活動(dòng)開始后，實(shí)際每天比原計(jì)劃每天多植樹50棵，實(shí)際植樹400棵所需時(shí)間與原計(jì)劃植樹300棵所需時(shí)間相同．設(shè)實(shí)際每天植樹x棵，則下列方程正確的是（　　）

  A． 400 x - 50 = 300 x	B． 300 x - 50 = 400 x
  C． 400 x + 50 = 300 x	D． 300 x + 50 = 400 x
  組卷：1912引用：32難度：0.8

  解析

• 7．一元二次方程x²+x-1=0的根的情況是（　　）

  A．有兩個(gè)不相等的實(shí)數(shù)根	B．沒有實(shí)數(shù)根
  C．有兩個(gè)相等的實(shí)數(shù)根	D．只有一個(gè)實(shí)數(shù)根
  組卷：1130引用：18難度：0.7

  解析

• 8．在平面直角坐標(biāo)系中，一次函數(shù)y=5x+1的圖象與y軸的交點(diǎn)的坐標(biāo)為（　　）

  A．（0，-1）

  B．（- 1 5 ，0）

  C．（ 1 5 ，0）

  D．（0，1）
  組卷：1133引用：9難度：0.7

  解析

三.解答題（將解答過程寫在答題卡上指定的位置，本大題共有9小題，計(jì)75分.）

• 23．（1）如圖1，在△ABC中，∠ACB=2∠B，CD平分∠ACB，交AB于點(diǎn)D，DE∥AC，交BC于點(diǎn)E．
  ①若DE=1，BD=

  3

  2

  ，求BC的長；
  ②試探究

  AB

  AD

  -

  BE

  DE

  是否為定值．如果是，請(qǐng)求出這個(gè)定值；如果不是，請(qǐng)說明理由．
  （2）如圖2，∠CBG和∠BCF是△ABC的2個(gè)外角，∠BCF=2∠CBG，CD平分∠BCF，交AB的延長線于點(diǎn)D，DE∥AC，交CB的延長線于點(diǎn)E．記△ACD的面積為S₁，△CDE的面積為S₂，△BDE的面積為S₃．若S₁?S₃=

  9

  16

  S

  2

  2

  ，求cos∠CBD的值．
  
  組卷：4072引用：8難度：0.3

  解析

• 24．如圖1，隧道截面由拋物線的一部分AED和矩形ABCD構(gòu)成，矩形的一邊BC為12米，另一邊AB為2米．以BC所在的直線為x軸，線段BC的垂直平分線為y軸，建立平面直角坐標(biāo)系xOy,規(guī)定一個(gè)單位長度代表1米．E（0，8）是拋物線的頂點(diǎn)．
  （1）求此拋物線對(duì)應(yīng)的函數(shù)表達(dá)式；
  （2）在隧道截面內(nèi)（含邊界）修建“”型或“”型柵欄，如圖2、圖3中粗線段所示，點(diǎn)P₁，P₄在x軸上，MN與矩形P₁P₂P₃P₄的一邊平行且相等．柵欄總長l為圖中粗線段P₁P₂，P₂P₃，P₃P₄，MN長度之和，請(qǐng)解決以下問題：
  （ⅰ）修建一個(gè)“”型柵欄，如圖2，點(diǎn)P₂，P₃在拋物線AED上．設(shè)點(diǎn)P₁的橫坐標(biāo)為m（0＜m≤6），求柵欄總長l與m之間的函數(shù)表達(dá)式和l的最大值；
  （ⅱ）現(xiàn)修建一個(gè)總長為18的柵欄，有如圖3所示的“”型和“”型兩種設(shè)計(jì)方案，請(qǐng)你從中選擇一種，求出該方案下矩形P₁P₂P₃P₄面積的最大值，及取最大值時(shí)點(diǎn)P₁的橫坐標(biāo)的取值范圍（P₁在P₄右側(cè)）．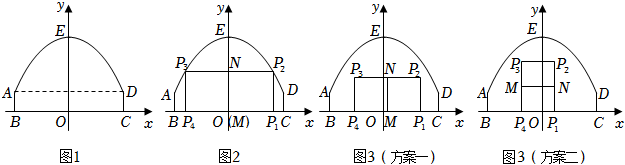
  
  組卷：2842引用：5難度：0.4

  解析