2023-2024學年山東省青島二中高三（上）期初數(shù)學試卷（8月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x＜2}，B={x|x²-2x-3≤0}，則A∪B=（　　）

  A．[-1，2）

  B．（2，3]

  C．（-1，3]

  D．（-∞，3]
  組卷：198引用：2難度：0.7

  解析

• 2．設復數(shù)z滿足iz=1+2i,則復數(shù)z的共軛復數(shù)

  z

  在復平面內(nèi)對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：35引用：5難度：0.9

  解析

• 3．已知非零向量

  a

  ，

  b

  滿足

  （

  a

  +

  2

  b

  ）

  ⊥

  （

  a

  -

  2

  b

  ）

  ，且向量

  a

  在向量

  b

  方向的投影向量是

  3

  b

  ，則向量

  a

  與

  b

  的夾角是（　　）

  A． π 6

  B． π 3

  C． π 2

  D． 2 π 3
  組卷：76引用：1難度：0.8

  解析

• 4．已知cosα=

  3

  5

  ，

  α

  ∈

  （

  3

  2

  π

  ，

  2

  π

  ）

  ，則sin

  α

  2

  =（　　）

  A． 5 5

  B．- 5 5

  C． 4 5

  D． 2 5 5
  組卷：942引用：5難度：0.7

  解析

• 5．若直線a,l,平面α滿足a?α，l?α，則“l(fā)⊥a”是“l(fā)⊥α”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：216引用：2難度：0.7

  解析

• 6．社區(qū)居委會計劃將6名志愿者平均分成3組，到3個不同地點服務，若每組去一個地點，每個地點都有人服務，且甲、乙兩名志愿者在同一個地點服務的分配方案有（　　）

  A．18種

  B．36種

  C．72種

  D．144種
  組卷：86引用：1難度：0.7

  解析

• 7．已知動點M在直線l₁：2x+2y-1=0上，動點N在直線l₂：2x+2y+1=0上，記線段MN的中點為P，圓C₁：x²+y²-2x-2y+1=0，圓C₂：x²+y²-4x-2y+1=0，A，B分別是圓C₁，C₂上的動點．則|PA|+|PB|的最小值為（　　）

  A．3

  B． 5 2 2

  C． 14 - 3

  D． 13 - 3
  組卷：146引用：1難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟

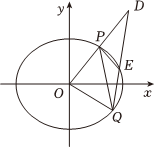• 21．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  1

  2

  ，左、右焦點分別為F₁，F(xiàn)₂，直線x=m與橢圓C交于A，B兩點，且△ABF₁的周長最大值為8．
  （1）求橢圓C的標準方程；
  （2）如圖，P，Q是橢圓C上的兩點，且直線OP與OQ的斜率之積為

  -

  3

  4

  （O為坐標原點），D為射線OP上一點，且|OP|=|PD|，線段DQ與橢圓C交于點E，

  |

  QE

  |

  =

  2

  3

  |

  ED

  |

  ，求四邊形OPEQ的面積．
  組卷：290引用：3難度：0.1

  解析

• 22．已知函數(shù)f（x）=xe^x-asinx（a∈R）．
  （1）當a=0時，求函數(shù)f（x）的極值；
  （2）若?x∈[0，π]，f（x）≥0，求a的取值范圍；
  （3）當a≥-3e³時，試討論f（x）在（0，2π）內(nèi)零點的個數(shù)，并說明理由．
  組卷：85引用：3難度：0.3

  解析