當前位置：試卷中心 > 試卷詳情

2022-2023學年四川省成都市蓉城名校聯盟高二（上）期末數學試卷（文科）

發布：2025/1/3 11:0:9

1．命題“?x∈N，3^x＞sinx”的否定是（　　）
A．?x∈N，3^x≤sinx B．?x∈N，3^x＜sinx
C．
?
x
0
∈
N
，
3
x
0
＞
sin
x
0
D．
?
x
0
∈
N
，
3
x
0
≤
sin
x
0
組卷：83引用：2難度：0.9
解析
2．直線
x
-
y
+
5
=
0
的傾斜角為（　　）
A．
π
6
B．
π
4
C．
π
3
D．
3
π
4
組卷：77引用：3難度：0.8
解析
3．拋物線y²=36x的準線方程是（　　）
A．y=9 B．y=-9 C．x=9 D．x=-9
組卷：49引用：2難度：0.7
解析
4．在空間直角坐標系O-xyz中，點A（-2，1，4）與A'（2，1，4）關于（　　）對稱．
A．xOy平面 B．yOz平面 C．xOz平面 D．原點
組卷：44引用：2難度：0.9
解析
5．某程序框圖如圖所示，則輸出的S=（　　）
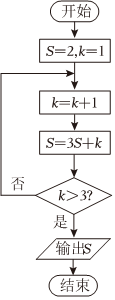
A．8 B．27 C．85 D．260
組卷：64引用：6難度：0.8
解析
6．若x,y滿足約束條件
x
+
5
y
-
8
≥
0
2
x
-
3
y
+
10
≥
0
3
x
+
2
y
-
11
≤
0
，則z=x+y的最大值為（　　）
A．0 B．4 C．5 D．2
組卷：55引用：1難度：0.7
解析
7．已知命題p：直線ax+3y-4=0與x+（a+2）y+2=0平行，命題q：a=-3，則p是q的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：124引用：2難度：0.7
解析

21．已知動點M到點F（1，0）的距離等于它到直線x=-1的距離，記動點M的軌跡為曲線C．
（1）求動點M的軌跡方程C；
（2）已知A（-2，0），過點B（0，1）的直線l斜率存在且不為0，若l與曲線C有且只有一個公共點P，求△PAB的面積．
組卷：137引用：1難度：0.6
解析
22．已知F₁，F₂分別為橢圓C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點，橢圓C的上頂點到右焦點的距離為2，右焦點F₂與拋物線y²=4x的焦點重合．
（1）求橢圓C的標準方程；
（2）已知點A（-2，0），斜率為k的動直線l與橢圓C交于P，Q兩點（P，Q均異于點A），且滿足k（k_AP+k_AQ）=-3，求證：直線l過定點．
組卷：62引用：1難度：0.6
解析

A．?x∈N，3^x≤sinx	B．?x∈N，3^x＜sinx
C． ? x 0 ∈ N ， 3 x 0 ＞ sin x 0	D． ? x 0 ∈ N ， 3 x 0 ≤ sin x 0

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

1．命題“?x∈N，3x＞sinx”的否定是（ ）