當前位置：試卷中心 > 試卷詳情

2023-2024學年廣東省四校聯考高三（上）月考數學試卷（9月份）

發布：2024/8/16 15:0:1

一、單選題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

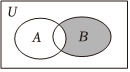1．已知全集U=R，集合A={x|x≥2或x≤-3}，B={x|0≤x≤4}，則Venn圖中陰影部分表示的集合為（　　）
A．[0，2） B．[0，3） C．（2，4] D．（3，4]
組卷：236引用：6難度：0.7
解析
2．函數
y
=
（
1
2
）
x
2
-
3
x
+
2
的單調遞增區間是（　　）
A．（-∞，1] B．[1，2] C．
[
3
2
，
+
∞
）
D．
（
-
∞
，
3
2
]
組卷：96引用：3難度：0.7
解析
3．在等差數列{a_n}中，a₆，a₁₈是方程x²-8x-17=0的兩個根，則{a_n}的前23項的和為（　　）
A．-184 B．-92 C．92 D．184
組卷：302引用：5難度：0.7
解析
4．設命題甲：?x∈R，x²+2ax+1＞0是真命題；命題乙：函數y=log_2a-1x在（0，+∞）上單調遞減是真命題，那么甲是乙的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：58引用：4難度：0.6
解析
5．已知函數f（x）=log_a（x-b）（a＞0且a≠1）的圖像如圖所示，則以下說法正確的是（　　）
A．a+b＜0 B．ab＜-1 C．0＜a^b＜1 D．log_a|b|＞0
組卷：652引用：5難度：0.9
解析
6．已知函數
f
（
x
）
=
x
2
-
ax
+
5
，
（
x
≤
1
）
a
x
，
（
x
＞
1
）
滿足對任意實數x₁≠x₂，都有
f
（
x
2
）
-
f
（
x
1
）
x
2
-
x
1
＜
0
成立，則a的取值范圍是（　　）
A．0＜a≤3 B．a≥2 C．a＞0 D．2≤a≤3
組卷：344引用：20難度：0.7
解析
7．若a=0.2^0.2，b=0.3^0.3，c=log_0.30.2，則（　　）
A．a＞b＞c B．b＞a＞c C．c＞a＞b D．c＞b＞a
組卷：73引用：5難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明，證明過程或演算步驟.

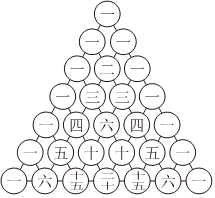21．在人教版高中數學教材選擇性必修三中，我們探究過“楊輝三角”（如圖所示）所蘊含的二項式系數性質，也了解到在我國古代，楊輝三角是解決很多數學問題的有力工具．
（1）把“楊輝三角”中第三斜列各數取出，并按原來的順序排列可得一數列{a_n}：1，3，6，10，15，…，請寫出a_n與a_n-1（n∈N^*，n≥2）的遞推關系，并求出數列{a_n}的通項公式；
（2）設
b
n
=
a
n
（
n
+
1
）
?
2
n
-
1
，證明：b₁+b₂+b₃+?+b_n＜2．
組卷：44引用：3難度：0.4
解析
22．已知函數f（x）=xlnx-x,g（x）=alnx-x²+1．
（1）求函數f（x）的最小值；
（2）若g（x）≤0在（0，+∞）上恒成立，求實數a的值；
（3）證明：
e
1
+
1
2
+
1
3
+
…
+
1
2022
＞
2023
，e是自然對數的底數．
組卷：129引用：3難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

2023-2024學年廣東省四校聯考高三（上）月考數學試卷（9月份）

一、單選題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知全集U=R，集合A={x|x≥2或x≤-3}，B={x|0≤x≤4}，則Venn圖中陰影部分表示的集合為（ ）

2．函數y=（12）x2-3x+2的單調遞增區間是（ ）

3．在等差數列{an}中，a6，a18是方程x2-8x-17=0的兩個根，則{an}的前23項的和為（ ）

4．設命題甲：?x∈R，x2+2ax+1＞0是真命題；命題乙：函數y=log2a-1x在（0，+∞）上單調遞減是真命題，那么甲是乙的（ ）

5．已知函數f（x）=loga（x-b）（a＞0且a≠1）的圖像如圖所示，則以下說法正確的是（ ）

6．已知函數f（x）=x2-ax+5，（x≤1）ax，（x＞1）滿足對任意實數x1≠x2，都有f（x2）-f（x1）x2-x1＜0成立，則a的取值范圍是（ ）

7．若a=0.20.2，b=0.30.3，c=log0.30.2，則（ ）

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明，證明過程或演算步驟.

22．已知函數f（x）=xlnx-x,g（x）=alnx-x2+1．（1）求函數f（x）的最小值；（2）若g（x）≤0在（0，+∞）上恒成立，求實數a的值；（3）證明：e1+12+13+…+12022＞2023，e是自然對數的底數．

1．已知全集U=R，集合A={x|x≥2或x≤-3}，B={x|0≤x≤4}，則Venn圖中陰影部分表示的集合為（　　）

2．函數
y
=
（
1
2
）
x
2
-
3
x
+
2
的單調遞增區間是（　　）

3．在等差數列{a_n}中，a₆，a₁₈是方程x²-8x-17=0的兩個根，則{a_n}的前23項的和為（　　）

4．設命題甲：?x∈R，x²+2ax+1＞0是真命題；命題乙：函數y=log_2a-1x在（0，+∞）上單調遞減是真命題，那么甲是乙的（　　）

5．已知函數f（x）=log_a（x-b）（a＞0且a≠1）的圖像如圖所示，則以下說法正確的是（　　）

6．已知函數
f
（
x
）
=
x
2
-
ax
+
5
，
（
x
≤
1
）
a
x
，
（
x
＞
1
）
滿足對任意實數x₁≠x₂，都有
f
（
x
2
）
-
f
（
x
1
）
x
2
-
x
1
＜
0
成立，則a的取值范圍是（　　）

7．若a=0.2^0.2，b=0.3^0.3，c=log_0.30.2，則（　　）

22．已知函數f（x）=xlnx-x,g（x）=alnx-x²+1．
（1）求函數f（x）的最小值；
（2）若g（x）≤0在（0，+∞）上恒成立，求實數a的值；
（3）證明：
e
1
+
1
2
+
1
3
+
…
+
1
2022
＞
2023
，e是自然對數的底數．