當前位置：試卷中心 > 試卷詳情

2021-2022學年浙江省杭州市桐廬中學創新班高一（上）期中數學試卷

發布：2024/10/21 8:0:1

一、選擇題（每小題5分，共50分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．已知全集U={1，2，3，4，5}，集合M={1，2}，N={3，4}，則?_U（M∪N）=（　　）
A．{5} B．{1，2} C．{3，4} D．{1，2，3，4}
組卷：3777引用：39難度：0.9
解析
2．已知命題p：?x∈（0，+∞），x＞lnx,則p的否定是（　　）
A．?x₀∈（0，+∞），x₀≤lnx₀ B．?x∈（0，+∞），x≤lnx₀
C．?x₀∈（0，+∞），x₀＞lnx₀ D．?x∈（0，+∞），x＜lnx₀
組卷：3引用：1難度：0.8
解析
3．若750°角的終邊上有一點P（a,3），則a的值是（　　）
A．
3
B．3
3
C．-
3
D．-3
3
組卷：24引用：1難度：0.5
解析
4．函數f（x）=（1-
2
1
+
e
x
）sinx的圖象的大致形狀是（　　）
A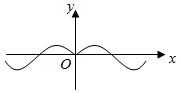． B．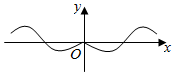
C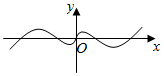． D．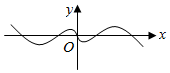
組卷：483引用：16難度：0.8
解析
5．已知函數
f
（
x
）
=
x
2
x
-
4
x
，則函數
f
（
x
-
1
）
x
+
1
的定義域為（　　）
A．（-∞，1） B．（-∞，-1）
C．（-∞，-1）∪（-1，0） D．（-∞，-1）∪（-1，1）
組卷：1243引用：7難度：0.7
解析
6．若向量
a
=
（
sin
2
α
，
cosα
）
，
b
=
（
1
，
cosα
）
，且
tanα
=
1
2
，則
a
?
b
的值是（　　）
A．
4
5
B．
6
5
C．
8
5
D．2
組卷：2引用：1難度：0.7
解析
7．函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）

（
A
＞
0

，

ω
＞
0

，

|
φ
|
＜
π
2
）
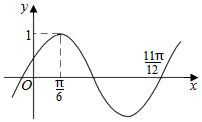的部分圖象如圖所示，則將y=f（x）的圖象向右平移
π
6
個單位后，得到的函數圖象的解析式為（　　）
A．y=sin2x B．
y
=
sin
（
2
x
+
2
π
3
）
C．
y
=
sin
（
2
x
-
π
6
）
D．y=cos2x
組卷：857引用：9難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四.解答題：本大題共5小題，共60分．解答應寫出文字說明，證明過程或演算步驟．

22．為了凈化空氣，某科研單位根據實驗得出，在一定范圍內，每噴灑1個單位的凈化劑，空氣中釋放的濃度y（單位：毫克/立方米）隨著時間x（單位：小時）變化的函數關系式近似為
y
=
16
9
-
2
x
-
1
，
0
≤
x
≤
3
16
-
2
x
-
3
，
3
＜
x
≤
7
．若多次噴灑，則某一時刻空氣中的凈化劑濃度為每次投放的凈化劑在相應時刻所釋放的濃度之和，由實驗知，當空氣中凈化劑的濃度不低于4（毫克/立方米）時，它才能起到凈化空氣的作用．
（1）若一次噴灑4個單位的凈化劑，則凈化時間約達幾小時？（結果精確到0.1，參考數據：lg2≈0.3，lg15≈1.17）
（2）若第一次噴灑2個單位的凈化劑，3小時后再噴灑2個單位的凈化劑，設第二次噴灑t小時后空氣中凈化劑濃度為g（t）（毫克/立方米），其中0＜1≤3．
①求g（t）的表達式；
②求第二次噴灑后的3小時內空氣中凈化劑濃度的最小值．
組卷：127引用：7難度：0.5
解析
23．已知函數
f
（
x
）
=
x
+
a
x
，g（x）=-2x²+（x-a）|x-a|+a²+3（a∈R）．
（1）當a=3時，求g（x）的單調區間；
（2）對?x₀∈[1，3]，?x₁，x₂∈[0，3]（x₁≠x₂），使得f（x₀）=g（x_i）（i=1，2），求實數a的取值范圍．
組卷：88引用：2難度：0.2
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．?x₀∈（0，+∞），x₀≤lnx₀	B．?x∈（0，+∞），x≤lnx₀
C．?x₀∈（0，+∞），x₀＞lnx₀	D．?x∈（0，+∞），x＜lnx₀

A．（-∞，1）	B．（-∞，-1）
C．（-∞，-1）∪（-1，0）	D．（-∞，-1）∪（-1，1）

A．y=sin2x	B． y = sin （ 2 x + 2 π 3 ）
C． y = sin （ 2 x - π 6 ）	D．y=cos2x

A．	B．
C．	D．

2021-2022學年浙江省杭州市桐廬中學創新班高一（上）期中數學試卷

一、選擇題（每小題5分，共50分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．已知全集U={1，2，3，4，5}，集合M={1，2}，N={3，4}，則?U（M∪N）=（ ）

2．已知命題p：?x∈（0，+∞），x＞lnx,則p的否定是（ ）

3．若750°角的終邊上有一點P（a,3），則a的值是（ ）

4．函數f（x）=（1-21+ex）sinx的圖象的大致形狀是（ ）

5．已知函數f（x）=x2x-4x，則函數f（x-1）x+1的定義域為（ ）

6．若向量a=（sin2α，cosα），b=（1，cosα），且tanα=12，則a?b的值是（ ）

7．函數f（x）=Asin（ωx+φ） （A＞0 ， ω＞0 ， |φ|＜π2）的部分圖象如圖所示，則將y=f（x）的圖象向右平移π6個單位后，得到的函數圖象的解析式為（ ）

四.解答題：本大題共5小題，共60分．解答應寫出文字說明，證明過程或演算步驟．

23．已知函數f（x）=x+ax，g（x）=-2x2+（x-a）|x-a|+a2+3（a∈R）．（1）當a=3時，求g（x）的單調區間；（2）對?x0∈[1，3]，?x1，x2∈[0，3]（x1≠x2），使得f（x0）=g（xi）（i=1，2），求實數a的取值范圍．

1．已知全集U={1，2，3，4，5}，集合M={1，2}，N={3，4}，則?_U（M∪N）=（　　）

2．已知命題p：?x∈（0，+∞），x＞lnx,則p的否定是（　　）

3．若750°角的終邊上有一點P（a,3），則a的值是（　　）

4．函數f（x）=（1-
2
1
+
e
x
）sinx的圖象的大致形狀是（　　）

5．已知函數
f
（
x
）
=
x
2
x
-
4
x
，則函數
f
（
x
-
1
）
x
+
1
的定義域為（　　）

6．若向量
a
=
（
sin
2
α
，
cosα
）
，
b
=
（
1
，
cosα
）
，且
tanα
=
1
2
，則
a
?
b
的值是（　　）

7．函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）

（
A
＞
0

，

ω
＞
0

，

|
φ
|
＜
π
2
）
的部分圖象如圖所示，則將y=f（x）的圖象向右平移
π
6
個單位后，得到的函數圖象的解析式為（　　）

23．已知函數
f
（
x
）
=
x
+
a
x
，g（x）=-2x²+（x-a）|x-a|+a²+3（a∈R）．
（1）當a=3時，求g（x）的單調區間；
（2）對?x₀∈[1，3]，?x₁，x₂∈[0，3]（x₁≠x₂），使得f（x₀）=g（x_i）（i=1，2），求實數a的取值范圍．