2023年湖北省荊州市沙市區中考數學調研試卷（5月份）

一、選擇題(本大題共10小題,每小題3分,共30分)

• 1．溫度由-4℃上升7℃是（　　）

  A．3℃

  B．-3℃

  C．11℃

  D．-11℃
  組卷：2633引用：43難度：0.9

  解析

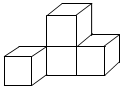• 2．如圖是一個由4個相同正方體組成的立體圖形，它的主視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：26引用：3難度：0.8

  解析

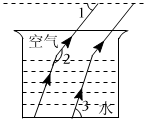• 3．如圖，光在不同介質中的傳播速度是不同的，因此當光線從水中射向空氣時，要發生折射．由于折射率相同，所以在水中平行的光線在空氣中也是平行的．如圖，∠1=48°，∠2=158°，則∠3的度數為（　　）

  A．68°

  B．70°

  C．88°

  D．80°
  組卷：95引用：1難度：0.6

  解析

• 4．下列說法正確的是（　　）

  A．為了解近十年全國初中生的肥胖人數變化趨勢，采用扇形統計圖最合適

  B．“煮熟的鴨子飛了”是一個隨機事件

  C．一組數據的中位數可能有兩個

  D．為了解我省中學生的睡眠情況，應采用抽樣調查的方式
  組卷：396引用：6難度：0.7

  解析

• 5．某氣球內充滿了一定質量m的氣體，當溫度不變時，氣球內氣體的氣壓p（單位：kPa）是氣體體積V（單位：m³）的反比例函數：p=

  m

  V

  ，能夠反映兩個變量p和V函數關系的圖象（　　）

  A．

  B．

  C．

  D．
  組卷：159引用：1難度：0.5

  解析

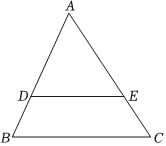• 6．如圖，平行于BC的直線DE把△ABC分為面積相等的兩部分，則DE：BC的值為 （　　）

  A．1：2

  B．2：3

  C． 2 ： 2

  D． 2 2 ： 2
  組卷：217引用：2難度：0.7

  解析

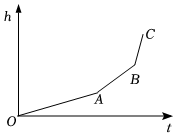• 7．勻速地向一個容器內注水，最后把容器注滿．在注水過程中，水面高度h隨時間t的變化規律如圖所示（圖中OABC為一折線）．這個容器的形狀可能是（　　）

  A．

  B．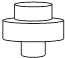

  C．

  D．
  組卷：2310引用：22難度：0.6

  解析

• 8．《九章算術》勾股章有一“引葭赴岸”問題：“今有池方一丈，葭生其中央，出水一尺，引葭赴岸，適與岸齊．問：水深，葭長各幾何．”意思是：如示意圖，有一個水池，水面是一個邊長為1丈的正方形，在水池正中央有一根蘆葦，它高出水面1尺，如果把這根蘆葦拉向水池一邊的中點，它的頂端恰好到達池邊的水面，水的深度和蘆葦的長度分別是多少？備注：1丈=10尺．設蘆葦長x尺，水的深度為y尺，則可列方程為（　　）

  A．x2+102=（x+1）2	B．（x-1）2+52=x2
  C．y2+52=（y-1）2	D．y2+102=（x+1）2
  組卷：222引用：2難度：0.7

  解析

解答題(本大題共有8小題,共72分

• 23．問題背景
  如圖（1），△ABD，△AEC都是等邊三角形，△ACD可以由△AEB通過旋轉變換得到，請寫出旋轉中心、旋轉方向及旋轉角的大小．
  嘗試應用
  如圖（2），在Rt△ABC中，∠ACB=90°，分別以AC，AB為邊，作等邊△ACD和等邊△ABE，連接ED，并延長交BC于點F，連接BD．若BD⊥BC，求

  DF

  DE

  的值．
  拓展創新
  如圖（3），在Rt△ABC中，∠ACB=90°，AB=2，將線段AC繞點A順時針旋轉90°得到線段AP，連接PB，直接寫出PB的最大值．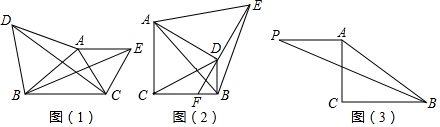
  
  組卷：4457引用：14難度：0.4

  解析

• 24．拋物線y=x²-4x與直線y=x交于原點O和點B，與x軸交于另一點A，頂點為D．
  （1）直接寫出點B和點D的坐標；
  （2）如圖1，連接OD，P為x軸上的動點，當tan∠PDO=

  1

  2

  時，求點P的坐標；
  （3）如圖2，M是點B關于拋物線對稱軸的對稱點，Q是拋物線上的動點，它的橫坐標為m（0＜m＜5），連接MQ，BQ，MQ與直線OB交于點E．設△BEQ和△BEM的面積分別為S₁和S₂，求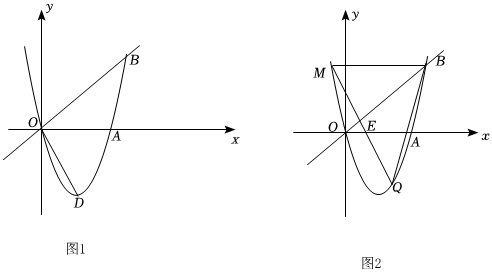

  S

  1

  S

  2

  的最大值．
  
  組卷：2519引用：7難度：0.2

  解析