2022年遼寧省沈陽市高考數學質檢試卷（三）

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知全集U={x∈N|-1＜x≤3}，A={1，2}，?_UA=（　　）

  A．{3}

  B．{0，3}

  C．{-1，3}

  D．{-1，0，3}
  組卷：417引用：1難度：0.9

  解析

• 2．已知復數z₁和z₂，則“z₁＞z₂”是“z₁-z₂＞0”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：195引用：3難度：0.8

  解析

• 3．在等比數列{a_n}中，a₂，a₈為方程x²-4x+π=0的兩根，則a₃a₅a₇的值為（　　）

  A． π π

  B． - π π

  C． ± π π

  D．π3
  組卷：395引用：2難度：0.7

  解析

• 4．中華民族傳統文化源遠流長，小明學習了二十四節氣歌后，打算在網上搜集一些與二十四節氣有關的古詩詞，他準備在冬季的6個節氣：立冬、小雪、大雪、冬至、小寒、大寒與春季的6個節氣：立春、雨水、驚蟄、春分、清明、谷雨這12個節氣中一共選出4個不同的節氣，搜集與之相關的古詩詞，如果冬季節氣和春季節氣各至少被選出1個，那么小明選取節氣的不同情況的種數是（　　）

  A．345

  B．465

  C．1620

  D．1860
  組卷：171引用：1難度：0.7

  解析

• 5．已知橢圓C：x²+4y²=m（m＞0）的兩個焦點分別為F₁，F₂，點P是橢圓上一點，若

  P

  F

  1

  ?

  P

  F

  2

  的最小值為-1，則

  P

  F

  1

  ?

  P

  F

  2

  的最大值為（　　）

  A．4

  B．2

  C． 1 4

  D． 1 2
  組卷：448引用：1難度：0.4

  解析

• 6．若lna=-1，e^b=

  2

  ，3c=ln3，則a,b,c的大小關系為（　　）

  A．a＞c＞b

  B．b＞c＞a

  C．c＞b＞a

  D．a＞b＞c
  組卷：834引用：7難度：0.6

  解析

• 7．函數

  y

  =

  f

  （

  x

  ）

  ，

  x

  ∈

  （

  -

  π

  2

  ，

  π

  2

  ）

  ，若

  f

  （

  -

  x

  ）

  +

  sin

  2

  x

  1

  +

  cos

  2

  x

  =

  0

  ，則f（x）在的圖象大致是（　　）

  A．

  B．

  C．

  D．
  組卷：69引用：1難度：0.8

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數

  f

  （

  x

  ）

  =

  xcosx

  +

  1

  4

  x

  2

  ，f′（x）為f（x）的導函數．
  （1）若

  x

  ∈

  [

  0

  ，

  π

  2

  ]

  ，

  f

  （

  x

  ）

  ≥

  m

  x

  2

  成立，求m的取值范圍；
  （2）證明：函數g（x）=f′（x）+cosx在

  （

  0

  ，

  π

  2

  ）

  上存在唯一零點．
  組卷：145引用：1難度：0.3

  解析

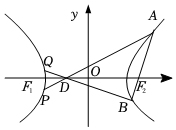• 22．如圖，在平面直角坐標系中，F₁，F₂分別為等軸雙曲線Γ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦點，若點A為雙曲線右支上一點，且

  |

  A

  F

  1

  |

  -

  |

  A

  F

  2

  |

  =

  4

  2

  ，直線AF₂交雙曲線于B點，點D為線段F₁O的中點，延長AD，BD，分別與雙曲線Γ交于P，Q兩點．
  （1）若A（x₁，y₁），B（x₂，y₂），求證：x₁y₂-x₂y₁=4（y₂-y₁）；
  （2）若直線AB，PQ的斜率都存在，且依次設為k₁，k₂，試判斷

  k

  2

  k

  1

  是否為定值，如果是，請求出

  k

  2

  k

  1

  的值；如果不是，請說明理由．
  組卷：660引用：3難度：0.3

  解析