2023年廣東省廣州大學附中教育集團自主招生數學試卷
發布:2024/11/2 11:0:2
一、單項選擇題(本大題共10小題,每小題3分,滿分30分,在每小題給出的四個選項中,只有一項是符合題目要求的)
-
1.已知m、n是方程x2+2020x+7=0的兩個根,則(m2+2019m+6)(n2+2021n+8)=( )
A.2021 B.2020 C.2012 D.2011 組卷:930引用:2難度:0.6 -
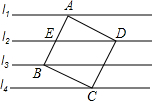 2.如圖,直線l1∥l2∥l3∥l4,相鄰兩條平行線間的距離都等于h,若正方形ABCD的四個頂點分別在四條直線上,則它的面積等于( )
2.如圖,直線l1∥l2∥l3∥l4,相鄰兩條平行線間的距離都等于h,若正方形ABCD的四個頂點分別在四條直線上,則它的面積等于( )A.4h2 B.5h2 C. 42h2D. 52h2組卷:711引用:2難度:0.7 -
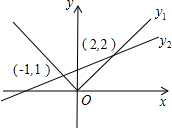 3.函數y1=|x|,.當y1>y2時,x的范圍是( )y2=13x+43
3.函數y1=|x|,.當y1>y2時,x的范圍是( )y2=13x+43A.x<-1 B.-1<x<2 C.x<-1或x>2 D.x>2 組卷:4698引用:44難度:0.9 -
4.已知x為實數,則
的最小值為( )x2-4x+13+x2+2x+2A.5 B. 10+5C. 3+5D.6 組卷:968引用:4難度:0.5 -
5.不等式組
的解集是關于x的一元一次不等式ax>-1解集的一部分,則a的取值范圍是( )2x+13-5x-36<1?①-5≤2x-1≤5?②A.0<a≤1 B. -13<a<0C. -13<a≤1D. 且a≠0.-13<a≤1組卷:907引用:2難度:0.5 -
6.求
的最小值( )|12x-1|+|13x-2|+|14x-3|A.12 B.6 C. 72D.3 組卷:1729引用:1難度:0.5 -
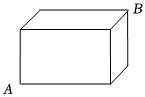 7.如圖,長方體的長、寬、高分別是8cm,2cm,4cm,一只螞蟻沿著長方體的表面從點A爬到點B,則螞蟻爬行的最短路徑長為( )
7.如圖,長方體的長、寬、高分別是8cm,2cm,4cm,一只螞蟻沿著長方體的表面從點A爬到點B,則螞蟻爬行的最短路徑長為( )A. 229B. 237C.10 D. 45+2組卷:343引用:1難度:0.6 -
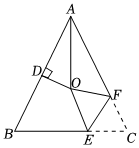 8.如圖,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分線與AB的垂直平分線交于點O,將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,則∠OEC的度數為( )
8.如圖,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分線與AB的垂直平分線交于點O,將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,則∠OEC的度數為( )A.72° B.100° C.108° D.120° 組卷:1307引用:8難度:0.7
四、解答題(本大題共3小題,滿分26分,解答應寫出文字說明、證明過程或演算步驟.)
-
23.如圖,在平面直角坐標系中,O為坐標原點,△ABC的邊BC在x軸上,A、B、C三點的坐標分別為A(0,m),B(-12,0),C(n,0),且(n-10)2+|3m-15|=0,一動點P從點B出發,以每秒2個單位長度的速度沿射線BO勻速運動,設點P運動時間為t秒.
(1)求A、C兩點的坐標;
(2)若點P恰好在∠BAO的角平分線上,求此時t的值;
(3)當點P在線段BO上運動時,在y軸上是否存在點Q,使△POQ與△AOC全等?若存在,請求出t的值并求出此時點Q的坐標;若不存在,請說明理由.
(4)連結PA,若△PAB為等腰三角形,請直接寫出點P的坐標. 組卷:357引用:2難度:0.2
組卷:357引用:2難度:0.2 -
24.四邊形ABCD是邊長為4的正方形,點E在邊AD所在直線上,連接CE,以CE為邊,作正方形CEFG(點D,點F在直線CE的同側),連接BF.
(1)如圖1,當點E與點A重合時,請直接寫出BF的長;
(2)如圖2,當點E在線段AD上時,AE=1;
①求點F到AD的距離;
②求BF的長;
(3)若BF=3,請直接寫出此時AE的長.10 組卷:6731引用:15難度:0.3
組卷:6731引用:15難度:0.3


