2023-2024學年黑龍江省大慶市薩爾圖區東風中學高二（上）月考數學試卷（10月份）

一、單選題（本大題共8小題，每題5分，共40分）

• 1．總體由編號01，02，…，19，20的20個個體組成．利用下面的隨機數表選取5個個體，選取方法是隨機數表第1行的第7列和第8列數字開始由左到右依次選取兩個數字，則選出來的第5個個體的編號為（　　）
  

  7816	6572	0802	6314	0702	4369	9728	0198
  3204	9234	4935	8200	3623	4869	6938	7481

  A．01

  B．02

  C．04

  D．07
  組卷：54引用：1難度：0.8

  解析

• 2．已知事件A，B滿足P（A）=0.5，P（B）=0.2，則（　　）

  A．若B?A，則P（AB）=0.5

  B．若A與B相互獨立，則P（A+B）=0.7

  C．若A與B相互獨立，則 P （ AB ） = 0 . 9

  D．若A與B互斥，則P（A+B）=0.7
  組卷：308引用：1難度：0.5

  解析

• 3．在100個零件中，有一級品20個，二級品30個，三級品50個，從中抽取20個作為樣本．
  方法一：采用簡單隨機抽樣的方法，將零件編號00，01，02，…，99，用抽簽法抽取20個．
  方法二：采用分層隨機抽樣的方法，從一級品中隨機抽取4個，從二級品中隨機抽取6個，從三級品中隨機抽取10個．
  對于上述問題，下列說法正確的是（　　）
  ①不論采用哪種抽樣方法，這100個零件中每一個零件被抽到的可能性都是

  1

  5

  ；
  ②采用不同的方法，這100個零件中每一個零件被抽到的可能性各不相同；
  ③在上述兩種抽樣方法中，方法2抽到的樣本比方法1抽到的樣本更能反映總體特征；
  ④在上述抽樣方法中，方法1抽到的樣本比方法2抽到的樣本更能反映總體的特征．

  A．①②

  B．①③

  C．①④

  D．②③
  組卷：140引用：2難度：0.8

  解析

• 4．已知數組

  a

  =（x,1，1），

  b

  =（-2，2，y），

  a

  ?

  b

  =0，則2x-y=（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：698引用：15難度：0.8

  解析

• 5．2023年夏天，國產動畫電影《長安三萬里》熱映，點燃“唐詩熱”，為此某市電視臺準備在該電視臺舉辦的“我愛背唐詩”前三屆參加總決賽的120名選手（假設每位選手只參加其中一屆總決賽）中隨機抽取24名參加一個唐詩交流會，若按前三屆參加總決賽的人數比例分層隨機抽樣，則第一屆抽取6人，若按性別比例分層隨機抽樣，則女選手抽取15人，則下列結論錯誤的是（　　）

  A．24是樣本容量

  B．第二屆與第三屆參加總決賽的選手共有90人

  C．120名選手中男選手有50人

  D．第一屆參加總決賽的女選手最多有30人
  組卷：78引用：3難度：0.7

  解析

• 6．在一段時間內，若甲去參觀市博物館的概率0.6，乙去參觀市博物館的概率為0.3，且甲乙兩人各自行動，則在這段時間內，甲乙兩人至少有一個去參觀博物館的概率是（　　）

  A．0.28

  B．0.36

  C．0.54

  D．0.72
  組卷：87引用：2難度：0.7

  解析

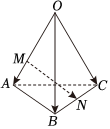• 7．如圖，在四面體OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ．點M在OA上，且OM=2MA，N為BC中點，則

  MN

  等于（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  組卷：438引用：74難度：0.7

  解析

四、解答題（本大題共6道題，共70分）

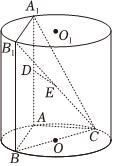• 21．如圖，AA₁，BB₁為圓柱OO₁的母線，BC是底面圓O的直徑，D，E分別是AA₁，CB₁的中點，DE⊥面CBB₁．
  ?（1）證明：AB⊥A₁C；
  （2）若BB₁=BC，求平面A₁B₁C與平面BDC的夾角余弦值．
  組卷：26引用：1難度：0.6

  解析

• 22．2021年孝感萬達廣場停車場臨時停車按時段收費，收費標準為每輛汽車一次停車不超過半小時的免費，超過半小時的部分每小時收費3元（不足1小時的部分按1小時計算）．現有甲、乙兩人在該停車場臨時停車，兩人停車時間互不影響且都不超過2.5小時．
  （1）若甲停車的時長在不超過半小時、半小時以上且不超過1.5小時、1.5小時以上且不超過2.5小時這三個時段的可能性相同，乙停車的時長在這三個時段的可能性也相同，求甲、乙兩人停車付費之和為6元的概率；
  （2）若甲、乙停車半小時以上且不超過1.5小時的概率分別為

  1

  4

  、

  1

  3

  ，停車1.5小時以上且不超過2.5小時的分別概率為

  5

  12

  、

  1

  6

  ，求甲、乙兩人臨時停車付費不相同的概率．
  組卷：289引用：7難度：0.6

  解析