2021年浙江省溫州市瑞安中學高考數學考前適應性試卷（5月份）

一、選擇題：本大題共10小題，每小題4分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x∈Z|-3＜x＜1}，B={y|y=2x,x∈A}，則A∩B的元素個數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：155引用：4難度：0.8

  解析

• 2．若復數z=

  m

  +

  i

  2

  -

  i

  （i是虛數單位）是純虛數，則實數m的值為（　　）

  A．-2

  B．- 1 2

  C． 1 2

  D．2
  組卷：80引用：2難度：0.8

  解析

• 3．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦點為F（2，0），漸近線方程為

  3

  x

  ±

  y

  =

  0

  ，則該雙曲線實軸長為（　　）

  A．2

  B．1

  C． 3

  D． 2 3
  組卷：136引用：2難度：0.7

  解析

• 4．若實數x,y滿足約束條件

  x - 2 y + 4 ≥ 0

  x + y + 1 ≥ 0

  x ≤ 2

  ，則z=3x+y的最大值為（　　）

  A．-5

  B．7

  C．9

  D．10
  組卷：55引用：1難度：0.6

  解析

• 5．等比數列{a_n}中，a₁＜0，則“a₂＜a₁”是“a₅＜a₆”的（　　）

  A．充要條件	B．必要不充分條件
  C．充分不必要條件	D．既不充分也不必要條件
  組卷：200引用：1難度：0.6

  解析

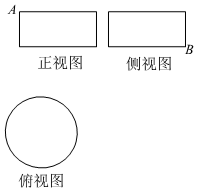• 6．某圓柱的高為2．底面周長為12，其三視圖如圖，圓柱表面上的點M在正視圖上對應點為A，圓柱表面上的點N在側視圖上對應點B，則在此圓柱側面上，從M到N的路徑中，最短路徑的長度為（　　）

  A． 13

  B．5

  C． 2 10

  D．8
  組卷：119引用：1難度：0.8

  解析

• 7．已知函數f（x）是定義在R上的奇函數，滿足f（x+2）=f（-x），且當x∈[0，1]時，f（x）=log₂（x+1），則函數y=f（x）-x³的零點個數是（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：476引用：3難度：0.6

  解析

三、解答題：本大題共5小題，共74分.解答應寫出文字說明、證明過程哦演算步驟

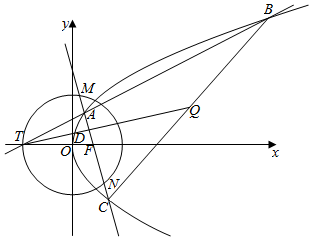• 21．已知拋物線C₁：y²=2px（p＞0）和右焦點為F的橢圓C₂：

  x

  2

  4

  +

  y

  2

  3

  =1．如圖，過橢圓C₂左頂點T的直線交拋物線C₁于A，B兩點，且

  AB

  =

  2

  TA

  ．連接AF交C₂于兩點M，N，交C₁于另一點C，連接BC，Q為BC的中點，TQ交AC于D．
  （Ⅰ）證明：點A的橫坐標為定值；
  （Ⅱ）記△CDT，△QMN的面積分別為S₁，S₂，若

  S

  1

  S

  2

  =

  5

  12

  ，求拋物線的方程．
  組卷：253引用：1難度：0.2

  解析

• 22．設a∈R，函數

  f

  （

  x

  ）

  =

  x

  -

  a

  e

  x

  +

  1

  e

  2

  x

  ．
  （Ⅰ）若a=2，求函數y=f（x）在x=0處的切線方程；
  （Ⅱ）若函數y=f（x）存在兩個不同的極值點，且x₀為函數f（x）的極大值點，求證：

  f

  （

  x

  0

  ）

  ＞

  1

  4

  ．
  組卷：108引用：1難度：0.4

  解析