2022-2023學年山東省青島第四實驗中學八年級（上）期末數學試卷

一、選擇題（本題滿分24分，共有8道小題，每小題3分）下列每小題都給出標號為A、B、C、D的四個結論，其中只有一個是正確的，每小題選對得分，不選、錯選或選出的標號超過一個的不得分

• 1．下列數中，哪一個是無理數（　　）

  A．3.1415926

  B． 2

  C． 3 - 8

  D． 3 2
  組卷：121引用：1難度：0.7

  解析

• 2．若x軸上的點P到y軸的距離為2，則點P的坐標為（　　）

  A．（2，0）	B．（2，0）或（-2，0）
  C．（0，2）	D．（0，2）或（0，-2）
  組卷：1458引用：6難度：0.7

  解析

• 3．下列各式中正確的是（　　）

  A． 9 =± 3

  B． x 2 = x

  C． 3 （ - x ） 3 = - x

  D． （ - x ） 2 = - x
  組卷：1496引用：8難度：0.7

  解析

• 4．△ABC中，∠A，∠B，∠C的對邊分別是a,b,c,下列結論中不正確的是（　　）

  A．如果∠A-∠B=∠C，那么△ABC是直角三角形，且c是斜邊

  B．如果a2=b2-c2，那么△ABC是直角三角形，且∠B是直角

  C．如果∠A：∠B：∠C=1：2：3，那么△ABC是直角三角形，且∠C是直角

  D．a2：b2：c2=9：16：25，那么△ABC是直角三角形，且c是斜邊
  組卷：944引用：2難度：0.7

  解析

• 5．已知一次函數y=kx+b（k≠0）的圖象與y軸負半軸相交，且函數值y隨自變量x的增大而減小，則一次函數y=bx-k的圖象大致是（　　）

  A．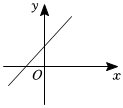

  B．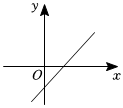

  C．

  D．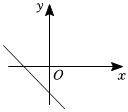
  組卷：484引用：1難度：0.6

  解析

• 6．若一組數據x₁，x₂，x₃，…，x_n的平均數為5，方差為4，則對于數據x₁-3，x₂-3，x₃-3，…，x_n-3，平均數和方差分別是（　　）

  A．2，1

  B．2，4

  C．5，4

  D．5，1
  組卷：530引用：4難度：0.7

  解析

• 7．現用190張鐵皮制作一批盒子，每張鐵皮可做8個盒身或做22個盒底，而一個盒身和兩個盒底配成一個完整的盒子．問用多少張白鐵皮制盒身、多少張白鐵皮制盒底，可以使盒身和盒底正好配套．設用x張鐵皮做盒身，y張鐵皮做盒底，可以使盒身與盒底正好配套，則可列方程是（　　）

  A． x + 2 y = 190 8 x = 22 y	B． x + y = 190 2 × 8 x = 22 y
  C． x + 2 y = 190 2 × 8 x = 22 y	D． x + y = 190 2 × 22 y = 8 x
  組卷：3386引用：17難度：0.7

  解析

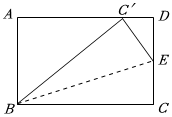• 8．如圖，在長方形ABCD中，AD=10cm,AB=6cm.將∠C沿BE折疊，使點C的對應點C'落在AD上，則DE的長度為（　　）

  A．2cm

  B．2.5cm

  C． 4 3 cm

  D． 8 3 cm
  組卷：309引用：1難度：0.6

  解析

三、解答題（本題共有8道小題，滿分72分）

• 24．如圖，直線y=-x+6分別與x軸、y軸交于A、B兩點．
  
  （1）A點的坐標

  、B點的坐標

  ；
  （2）已知點C坐標為（4，0），設點C關于直線AB的對稱點為D，請直接寫出點D的坐標；
  （3）請在直線AB上找一點P，使△OPC的周長最短，求出點P的坐標；
  （4）請在直線AB和y軸上分別找一點M、N使△CMN的周長最短，直接寫出最短周長．
  組卷：446引用：1難度：0.3

  解析

選做題（本題得分為附加分，不計入總成績）

• 25．介紹一個“能被13整除的數的特征”的數學小知識：一個多位數m（數位大于等于4）的末三位數與末三位數以前的數字所組成的數之差記為F（m），F（m）如果能被13整除，則這個多位數就一定能被13整除．例如數字160485，這個數末三位是485，末三位以前是160，F（m）=485-160=325，325÷13=25．即325能被13整除，那么160485也能被13整除．（注：這個規律也適用于11和7）
  （1）F（m）（60541）=

  ，60541

  （填能或不能）被13整除．
  （2）試證明這個“能被13整除的數的特征”的數學原理．
  （3）若m,n均為13的倍數，且m=1020+101a,n=1000b+c+230，（0≤a≤9，1≤b≤9，0≤c≤9，且a,b,c均為整數）．規定K（m,n）=

  b

  -

  c

  a

  ，當

  F

  （

  m

  ）

  13

  +

  F

  （

  n

  ）

  13

  =35時，直接寫出K（m,n）的值．
  組卷：168引用：1難度：0.5

  解析