2023-2024學年天津市河東區高三（上）期中數學試卷

一、單選題（本大題共9小題）

• 1．已知全集U=R，集合A={x|x²-x-6＞0}，B={x∈Z||x-1|＜3}，則（?_UA）∩B=（　　）

  A．（-1，3]

  B．[-1，3]

  C．{-1，0，1，2，3}

  D．{0，1，2，3}
  組卷：102引用：1難度：0.8

  解析

• 2．已知A={x|1≤x≤2}，命題“?x∈A，x²-a≤0”是真命題的一個充分不必要條件是（　　）

  A．a≥6

  B．a≥4

  C．a≤4

  D．a≤1
  組卷：67引用：1難度：0.9

  解析

• 3．函數

  f

  （

  x

  ）

  =

  xsinx

  +

  1

  x

  2

  -

  1

  π

  2

  在區間[-2π，2π]上的大致圖象為（　　）

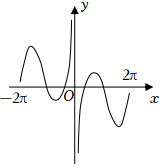
  A．	B．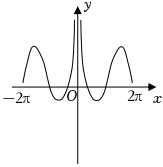
  C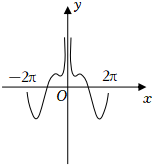．	D．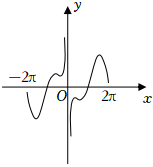
  組卷：166引用：10難度：0.8

  解析

• 4．設

  a

  =

  lo

  g

  3

  4

  （

  lo

  g

  3

  4

  ）

  ，

  b

  =

  （

  3

  4

  ）

  0

  .

  5

  ，

  c

  =

  （

  4

  3

  ）

  0

  .

  5

  ，則（　　）

  A．c＜b＜a

  B．c＜a＜b

  C．a＜b＜c

  D．a＜c＜b
  組卷：157引用：1難度：0.7

  解析

• 5．設等差數列{a_n}的前n項和為S_n，數列{b_n}的前n項和為T_n，已知a₅=11，s₁₀=120，b_n=

  1

  a

  n

  ?

  a

  n

  +

  1

  ，若T_k=

  8

  57

  ，則正整數k的值為（　　）

  A．9

  B．8

  C．7

  D．6
  組卷：106引用：5難度：0.6

  解析

• 6．為征求個人所得稅法修改建議，某機構調查了10000名當地職工的月收入情況，并根據所得數據畫出了樣本的頻率分布直方圖，
  下面三個結論：
  ①估計樣本的中位數為4850元；
  ②如果個稅起征點調整至6000元，估計有25%的當地職工會被征稅；
  ③根據此次調查，為使70%以上的職工不用繳納個人所得稅，起征點應調整至6500元．
  其中正確結論的個數有（　　）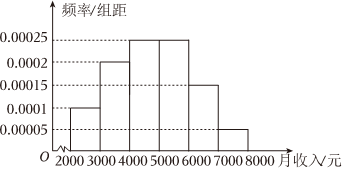
  

  A．0

  B．1

  C．2

  D．3
  組卷：108引用：1難度：0.7

  解析

三、解答題（本大題共5小題，解答應寫出文字說明，證明過程或演算步驟）

• 19．設數列{a_n}（n∈N*）是公差不為零的等差數列，滿足a₃+a₆=a₉，a₅+a₇²=6a₉；數列{b_n}（n∈N*）的前n項和為S_n，且滿足4S_n+2b_n=3．
  （1）求數列{a_n}、{b_n}的通項公式；
  （2）在b₁和b₂之間插入1個數x₁₁，使b₁，x₁₁，b₂成等差數列；在b₂和b₃之間插入2個數x₂₁，x₂₂，使b₂，x₂₁，x₂₂，b₃成等差數列；……；在b_n和b_n+1之間插入n個數x_n1，x_n2，…，x_nn，使b_n，x_n1，x_n2，…x_nn，b_n+1成等差數列．
  （i）求T_n=x₁₁+x₂₁+x₂₂+…+x_n1+x_n2+…+x_nn；
  （ii）是否存在正整數m,n,使T_n=

  a

  m

  +

  1

  2

  a

  m

  成立？若存在，求出所有的正整數對（m,n）；若不存在，請說明理由．
  組卷：1042引用：7難度：0.3

  解析

• 20．已知函數f（x）=xlnx-a（x-1），其中a∈R．
  （1）當a=1時，求函數f（x）在點（e,f（e））上的切線方程．（其中e為自然對數的底數）
  （2）已知關于x的方程

  f

  （

  x

  ）

  x

  +

  a

  =

  ax

  +

  a

  x

  有兩個不相等的正實根x₁，x₂，且x₁＜x₂．
  （ⅰ）求實數a的取值范圍；
  （ⅱ）設k為大于1的常數，當a變化時，若

  x

  k

  1

  x

  2

  有最小值e^e，求k的值．
  組卷：414引用：7難度：0.2

  解析