2022-2023學年湖北省荊州市八縣市高二（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．空間中點A（1，2，3）到點B（0，2，1）的距離為（　　）

  A．2

  B． 5

  C． 3

  D．3
  組卷：167引用：2難度：0.7

  解析

• 2．l₁：a²x-y+a²-3a=0，l₂：（4a-3）x-y-2=0，若l₁∥l₂，則a=（　　）

  A．1

  B．1或2

  C．1或3

  D．3
  組卷：158引用：4難度：0.7

  解析

• 3．已知正三棱柱A₁B₁C₁-ABC，M為棱BC上靠近點C的三等分點，則

  A

  1

  M

  =（　　）

  A． A 1 C 1 - C C 1 + 2 3 C 1 B 1	B． 1 2 A 1 C 1 + 1 2 A 1 B 1 + B 1 B
  C． A 1 C 1 + 1 3 C 1 B 1 + C 1 C	D． 1 3 A 1 C 1 + 2 3 AB + C 1 C
  組卷：119引用：2難度：0.7

  解析

• 4．若{a_n}的前n項和S_n=n³-2n²，則a₅+a₆=（　　）

  A．86

  B．112

  C．156

  D．84
  組卷：248引用：1難度：0.7

  解析

• 5．已知F₁，F₂分別為橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左右焦點，P為C上一動點，A為C的左頂點，若

  3

  P

  F

  1

  =

  2

  PA

  +

  P

  F

  2

  ，則C的離心率為（　　）

  A． 1 2

  B． 3 3

  C． 1 3

  D． 2 2
  組卷：173引用：3難度：0.7

  解析

• 6．公差不為0的等差數列{a_n}中，a₄-a_x=a_y-a₇，則xy的值不可能是（　　）

  A．10

  B．24

  C．22

  D．30
  組卷：164引用：1難度：0.7

  解析

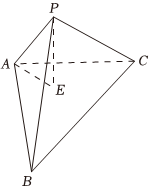• 7．如圖，已知三棱錐P-ABC的底面是以A為直角頂點，腰長為2的等腰三角形，且PA=1，E為P點在底面的投影，且BC⊥AE，PA與底面所成角為

  π

  4

  ，則該三棱錐外接球的體積為（　　）

  A． 5 10 3 π

  B． 8 2 3 π

  C． 8 3 π

  D． 4 3 π
  組卷：135引用：1難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知點A（1，

  3

  2

  ）為橢圓C

  ：

  x

  2

  a

  2

  +

  y

  2

  a

  2

  -

  1

  =

  1

  上的一點，B（-2，0）．
  （1）求C的方程；
  （2）若直線l交C于M，N兩點，連接BM，BN并延長，記直線BM，BN，l的斜率滿足k_MN（k_BM+k_BN）+3=0，證明：直線l恒過定點，并求出該定點的坐標．
  組卷：91引用：2難度：0.6

  解析

• 22．已知橢圓C：

  x

  2

  4

  +

  y

  2

  =

  1

  的左右頂點分別為A₁，A₂，直線x=m（0＜m＜2）與C交于M、N兩點，直線A₁M和直線A₂N交于點P．
  （1）求P點的軌跡方程；
  （2）求

  |

  P

  A

  1

  |

  ?

  |

  PM

  |

  |

  P

  A

  2

  |

  ?

  |

  PN

  |

  的取值范圍．
  組卷：50引用：2難度：0.5

  解析