當前位置：試卷中心 > 試卷詳情

2022-2023學年內蒙古呼和浩特市賽罕區八年級（下）期中數學試卷

發布：2024/7/14 8:0:9

1．下列式子，是最簡二次根式的是（　　）
A．
9
B．
20
C．
7
D．
1
3
組卷：183引用：5難度：0.8
解析
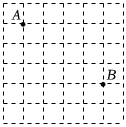2．如圖所示，在邊長為1的小正方形組成的網格中，點A，B都是格點，則線段AB的長是（　　）
A．5 B．
5
C．7 D．25
組卷：101引用：2難度：0.7
解析
3．下列計算正確的是（　　）
A．
25
=±
5
B．
（
-
2
）
2
=
-
2
C．
25
121
=
5
11
D．
a
2
=
（
a
）
2
組卷：88引用：2難度：0.8
解析
4．下列命題正確的是（　　）
A．形如
a
的式子叫做二次根式
B．一組鄰邊相等的矩形是正方形
C．對角線相等的四邊形是矩形
D．在直角三角形ABC中，三邊a,b,c滿足的關系是a²+b²=c²
組卷：28引用：2難度：0.7
解析
5．下列計算正確的有幾個（　　）
①
2
3
×
3
3
=
6
3
；
②
2
+
3
=
5
；
③
5
5
-2
2
=3
3
；
④
2
÷
3
=
6
3
．
A．4 B．3 C．2 D．1
組卷：62引用：2難度：0.7
解析
6．分別滿足下列條件的三角形不是直角三角形的是（　　）
A．三邊之比為
1
：
2
：
3
B．三邊長依次是9，40，41
C．三邊之比為
1
：
2
：
3
D．三內角之比為3：4：5
組卷：61引用：2難度：0.7
解析
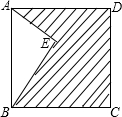7．如圖，點E在正方形ABCD內，滿足∠AEB=90°，AE=6，BE=8，則陰影部分的面積是（　　）
A．48 B．60 C．76 D．80
組卷：3535引用：139難度：0.9
解析

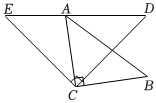22．已知△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的頂點A在△ECD的斜邊DE上，若AE=3，AD=4，求AC的長．
組卷：31引用：1難度：0.5
解析
23．“弦圖”不僅是證明勾股定理的一種方法，也是解決直角三角形問題可用的方法，請用弦圖的模型解決下列問題：
（1）用四個斜邊長為5，一條直角邊長為3的直角三角形如圖1所示的正方形ABCD和小正方形EFGH，求小正方形的對角線EG的長；
（2）如圖2，邊長為5的正方形內有兩個全等的直角三角形，一條直角邊CF=4，求兩個直角頂點這距離EF；
（3）已知Rt△ABC，∠C=90°，
AB
=
5
，BC=1，以AB為一直角邊作等腰直角三角形ABD，且BA=BD，點O是AD的中點，則CO=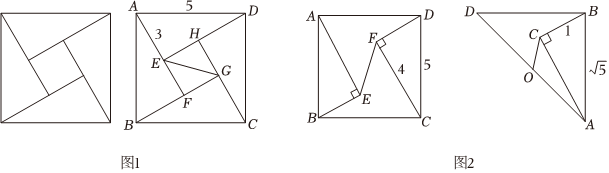
．
組卷：96引用：1難度：0.3
解析