2021年陜西省榆林市橫山區中考數學二模試卷

一、選擇題（共8小題，每小題3分，計24分，每小題只有一個選項是符合題意的）

• 1．一個數a的絕對值等于它本身，則a的值不可能是（　　）

  A．1

  B．-1

  C．0

  D．2
  組卷：40引用：2難度：0.9

  解析

• 2．如圖4個漢字中，可以看作是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：2引用：1難度：0.9

  解析

• 3．如圖，CD⊥AB于點D，點E為CD上一點，過點E作EF∥AB，連接CF，若∠C=50°，則∠F的度數為（　　）

  A．40°

  B．35°

  C．45°

  D．50°
  組卷：4引用：1難度：0.7

  解析

• 4．化簡x²-（x+2）（x-2）的結果是（　　）

  A．2x2-2

  B．x2-4

  C．2x2-4

  D．4
  組卷：24引用：2難度：0.7

  解析

• 5．如圖，以點O為位似中心，將△OAB放大后得到△OCD，若OA=3，AC=5，則△OAB與△OCD的面積比為（　　）

  A．3：5

  B．3：8

  C．9：64

  D．9：25
  組卷：14引用：2難度：0.6

  解析

• 6．已知直線y=-x-2沿x軸向左平移m個單位后，所得直線與直線y=x+4關于x軸對稱，則m的值為（　　）

  A．4

  B．3

  C．2

  D．1
  組卷：64引用：1難度：0.5

  解析

• 7．如圖，⊙O的半徑為3，點A為⊙O上一點，連接OA，以OA為一條直角邊Rt△OAB，使∠AOB=90°，OB=4，AB交⊙O于點C，則BC的長為 （　　）

  A． 7 5

  B． 12 5

  C． 18 5

  D． 36 5
  組卷：322引用：3難度：0.7

  解析

• 8．若P₁（x₁，y₁）、P₂（x₂，y₂）是拋物線y=ax²-4ax上兩點，當|x₁-2|＞|x₂-2|時，則下列表達式正確的是（　　）

  A．y1+y2＞0

  B．a（y1+y2）＞0

  C．y1-y2＞0

  D．a（y1-y2）＞0
  組卷：819引用：5難度：0.7

  解析

三、解答題（共12小題，計78分.解答應寫出過程）

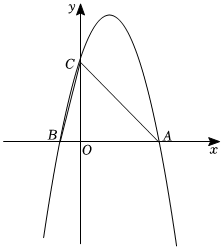• 25．如圖，拋物線y=ax²+bx+c（a、b、c為常數，且a≠0）與x軸交于A，B兩點，與y軸交于點C，已知OA=OC=4OB=4．
  （1）求拋物線的函數表達式；
  （2）連接BC，AC，若點D在x軸的下方，以A、B、D為頂點的三角形與△ABC全等，平移這條拋物線，使平移后的拋物線經過點B與點D，請求出平移后所得拋物線的函數表達式，并寫出平移過程．
  組卷：37引用：2難度：0.3

  解析

• 26．【問題提出】
  （1）如圖①，在平行四邊形ABCD中，對角線AC、BD相交于點O，若S_△ABC=3，則△ABD的面積為

  ；
  【問題探究】
  （2）如圖②，已知BC=6，點A為BC上方的一個動點，且∠BAC=120°，點D為BA延長線上一點，且AD=AC，連接CD，求△BCD面積的最大值；
  【問題解決】
  （3）如圖③，四邊形ABCD是規劃中的休閑廣場示意圖，AC、BD為兩條人行通道，根據規劃要求，人行通道AC的長為500米，∠DBC=30°，AD∥BC，為了容納更多的人，要求該休閑廣場的面積盡可能大，請問休閑廣場ABCD的面積是否存在最大值，如果存在，求出四邊形ABCD的最大面積，如果不存在，請說明理由．（結果保留根號）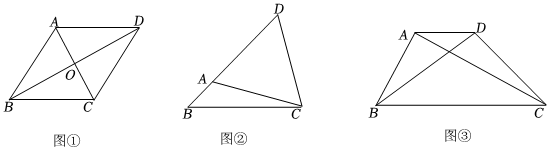
  
  組卷：140引用：2難度：0.3

  解析