2022-2023學(xué)年黑龍江省大慶市龍鳳區(qū)靚湖學(xué)校七年級(jí)（上）期中數(shù)學(xué)試卷

一、選擇題（每題3分，共30分）

• 1．用平面去截一個(gè)幾何體，如果截面的形狀是長(zhǎng)方形，那么該幾何體不可能是（　　）

  A．圓柱

  B．棱柱

  C．正方體

  D．圓錐
  組卷：399引用：11難度：0.5

  解析

• 2．下列語句正確的是（　　）
  ①一個(gè)數(shù)前面加上“-”號(hào)，這個(gè)數(shù)就是負(fù)數(shù)；
  ②如果a是正數(shù)，那么-a一定是負(fù)數(shù)；
  ③一個(gè)有理數(shù)不是正的就是負(fù)的；
  ④0°表示沒有溫度．

  A．0個(gè)

  B．1個(gè)

  C．2個(gè)

  D．3個(gè)
  組卷：336引用：5難度：0.8

  解析

• 3．有一個(gè)三位數(shù)，個(gè)位數(shù)字是x,十位數(shù)字是y,百位數(shù)字是z,現(xiàn)將這個(gè)三位數(shù)的百位數(shù)字和個(gè)位數(shù)字互換位置后的三位數(shù)是（　　）

  A．100z+10y+x

  B．100x+10y+z

  C．100y+10z+x

  D．x+y+z
  組卷：63引用：2難度：0.5

  解析

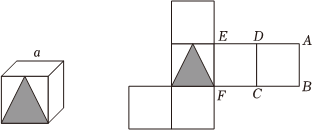• 4．將一個(gè)小正方體按圖中所示的方式展開，則在展開圖中表示棱a的線段可以是（　　）

  A．線段CD

  B．線段EF

  C．線段AD

  D．線段BC
  組卷：45引用：3難度：0.5

  解析

• 5．下列說法中不正確的是（　　）

  A．用平面去截正方體，能截出一個(gè)梯形

  B．有理數(shù)都能用數(shù)軸上的點(diǎn)表示

  C．最小的整數(shù)是0

  D．用平面去截正方體，能截出一個(gè)六邊形
  組卷：30引用：2難度：0.7

  解析

• 6．已知a,b,c三個(gè)數(shù)在數(shù)軸上對(duì)應(yīng)點(diǎn)的位置如圖所示，下列幾個(gè)判斷：①a＜b＜c；②-a＜b；③a+b＞0；④c-a＞0中，正確的個(gè)數(shù)是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：544引用：8難度：0.9

  解析

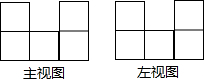• 7．一個(gè)幾何體是由若干個(gè)相同的立方體組成，其主視圖和左視圖如圖所示，則組成這個(gè)幾何體的立方體個(gè)數(shù)不可能的是（　　）

  A．15 個(gè)

  B．13 個(gè)

  C．11 個(gè)

  D．5 個(gè)
  組卷：312引用：8難度：0.7

  解析

• 8．已知y=ax⁵+bx³+cx-1，當(dāng)x=-2時(shí)y=5，則當(dāng)x=2時(shí)，y=（　　）

  A．-17

  B．-7

  C．-3

  D．7
  組卷：117引用：5難度：0.9

  解析

• 9．已知a,b,c為有理數(shù)，且滿足abc＜0，a+b+c=0，則

  |

  a

  |

  b

  +

  c

  +

  |

  b

  |

  a

  +

  c

  +

  |

  c

  |

  b

  +

  a

  的值為（　　）

  A．-1

  B．1，-1

  C．-1，3

  D．1，-1，3或-3
  組卷：210引用：4難度：0.5

  解析

四、解答題（共54分）

• 27．我們知道：1-

  1

  2

  =

  2

  1

  ×

  2

  -

  1

  1

  ×

  2

  =

  1

  1

  ×

  2

  ；

  1

  2

  -

  1

  3

  =

  3

  2

  ×

  3

  -

  2

  2

  ×

  3

  =

  1

  2

  ×

  3

  ；

  1

  3

  -

  1

  4

  =

  4

  3

  ×

  4

  -

  3

  3

  ×

  4

  =

  1

  3

  ×

  4

  ；…，
  反過來，可得：

  1

  1

  ×

  2

  =

  1

  -

  1

  2

  ；

  1

  2

  ×

  3

  =

  1

  2

  -

  1

  3

  ；

  1

  3

  ×

  4

  =

  1

  3

  -

  1

  4

  ；…，
  各式相加，可得：

  1

  1

  ×

  2

  +

  1

  2

  ×

  3

  +

  1

  3

  ×

  4

  =

  1

  -

  1

  2

  +

  1

  2

  -

  1

  3

  +

  1

  3

  -

  1

  4

  =

  1

  -

  1

  4

  =

  3

  4

  ．
  （1）直接寫出結(jié)果：

  1

  1

  ×

  2

  +

  1

  2

  ×

  3

  +

  1

  3

  ×

  4

  +

  1

  4

  ×

  5

  +

  1

  5

  ×

  6

  +

  1

  6

  ×

  7

  =

   

  ；
  （2）計(jì)算：

  1

  1

  ×

  5

  +

  1

  5

  ×

  9

  +

  1

  9

  ×

  13

  +

  …

  +

  1

  97

  ×

  101

  ；
  （3）計(jì)算：

  1

  1

  ×

  4

  ×

  7

  +

  1

  4

  ×

  7

  ×

  10

  +

  1

  7

  ×

  10

  ×

  13

  +

  …

  +

  1

  94

  ×

  97

  ×

  100

  ．
  組卷：233引用：3難度：0.3

  解析

• 28．唐代文學(xué)家韓愈曾賦詩：“天街小雨潤如酥，草色遙看近卻無”，當(dāng)代印度詩人泰戈?duì)栆矊懙溃骸笆澜缟献钸b遠(yuǎn)的距離，不是瞬間便無處尋覓；而是尚未相遇，便注定無法相聚”．距離是數(shù)學(xué)、天文學(xué)、物理學(xué)中的熱門話題，唯有對(duì)宇宙距離進(jìn)行測(cè)量，人類才能掌握世界尺度．已知點(diǎn)P，Q在數(shù)軸上分別表示有理數(shù)p,q,P，Q兩點(diǎn)之間的距離表示為PQ=|p-q|．例如，在數(shù)軸上，有理數(shù)3與1對(duì)應(yīng)的兩點(diǎn)之間的距離為|3-1|=2；有理數(shù)5與-2對(duì)應(yīng)的兩點(diǎn)之間的距離為|5-（-2）|=7；有理數(shù)-8與-5對(duì)應(yīng)的兩點(diǎn)之間的距離為|-8-（-5）|=3；…
  解決問題：
  （1）數(shù)軸上有理數(shù)-10與3對(duì)應(yīng)的兩點(diǎn)之間的距離等于

  ；數(shù)軸上有理數(shù)x與-5對(duì)應(yīng)的兩點(diǎn)之間的距離用含x的式子表示為

  ；若數(shù)軸上有理數(shù)x與1對(duì)應(yīng)的兩點(diǎn)A、B之間的距離|AB|=6，求x的值；
  聯(lián)系拓廣：
  （2）如圖，點(diǎn)M表示的數(shù)為4，點(diǎn)N表示的數(shù)為-2，p為數(shù)軸上的動(dòng)點(diǎn)，動(dòng)點(diǎn)P表示的數(shù)為x.
  
  ①若點(diǎn)在點(diǎn)M、N兩點(diǎn)之間，則|PM|+|PN|=

  ；若|PM|+|PN|=10，則點(diǎn)P表示的數(shù)x為

  ．
  由此可得：當(dāng)|x+3|+|x-7|取最小值時(shí)，求整數(shù)x的所有取值的和；
  ②當(dāng)點(diǎn)P到點(diǎn)M的距離等于點(diǎn)P到點(diǎn)N的距離的2倍時(shí)，求x的值．
  組卷：375引用：4難度：0.6

  解析