2022-2023學年廣東省惠州市惠陽區良井中學九年級（上）月考數學試卷（9月份）

一、選擇題（共10題，共30分）

• 1．用公式法解一元二次方程3x²-3x=1時，化方程為一般式，當中的a、b、c依次為（　　）

  A．3，-3，1

  B．3，-3，-1

  C．3，3，-1

  D．3，3，1
  組卷：537引用：3難度：0.8

  解析

• 2．下列拋物線中，與拋物線y=x²-2x+4具有相同對稱軸的是（　　）

  A．y=4x2+2x+1

  B．y=2x2-4x+1

  C．y=2x2-x+4

  D．y=x2-4x+2
  組卷：739引用：5難度：0.9

  解析

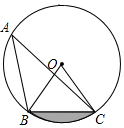• 3．如圖，點A、B、C在⊙O上，若∠BAC=30°，OB=2，則圖中陰影部分的面積為（　　）

  A． π 3 - 3

  B． 2 π 3 - 3

  C． 2 π 3 -2 3

  D． π 3 -2 3
  組卷：620引用：4難度：0.7

  解析

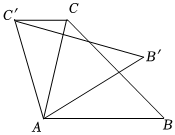• 4．如圖，在△ABC中，∠CAB=75°，在同一平面內，將△ABC繞點A旋轉到△AB′C′的位置，使得CC′∥AB，則∠BAB′=（　　）

  A．30°

  B．35°

  C．40°

  D．50°
  組卷：2556引用：62難度：0.7

  解析

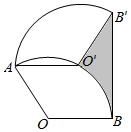• 5．如圖，將半徑為2，圓心角為120°的扇形OAB繞點A逆時針旋轉60°，點O，B的對應點分別為O′，B′，連接BB′，則圖中陰影部分的面積是（　　）

  A． 2 π 3

  B．2 3 - π 3

  C．2 3 - 2 π 3

  D．4 3 - 2 π 3
  組卷：1691引用：28難度：0.7

  解析

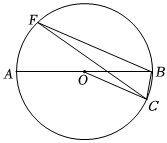• 6．如圖，AB為⊙O的直徑，點C為⊙O上一點，BF∥OC，若AB=10，BC=2，則CF=（　　）

  A．4

  B．5

  C． 4 6

  D．3
  組卷：6引用：2難度：0.7

  解析

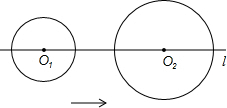• 7．如圖，⊙O₁，⊙O₂的圓心在直線l上，⊙O₁的半徑為2cm,⊙O₂的半徑為3cm.O₁O₂=8cm,⊙O₁以1cm/s的速度沿直線l向右運動，7s后停止運動．在此過程中，⊙O₁和⊙O₂沒有出現的位置關系是（　　）

  A．外切

  B．相交

  C．內切

  D．內含
  組卷：388引用：61難度：0.9

  解析

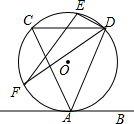• 8．如圖，直線AB與⊙O相切于點A，弦CD∥AB，E，F為圓上的兩點，且∠CDE=∠ADF．若⊙O的半徑為

  5

  2

  ，CD=4，則弦EF的長為（　　）

  A．4

  B．2 5

  C．5

  D．6
  組卷：2763引用：70難度：0.7

  解析

三、解答題（共8題，共62分）

• 24．如圖1，在三角形ABC中，把AB繞點A順時針旋轉90°得到AD，把AC繞點A逆時針旋轉90°，得到AE，連接DE，過點A作BC的垂線，交BC于點F，交DE于點G．
  【特例嘗試】如圖2，當∠BAC=90°時，
  ①求證：∠DAE=90°；
  ②猜想BC與AG的數量關系并說明理由．
  【理想論證】在圖1中，當△ABC為任意三角形時，②中BC與AG的數量關系還成立嗎？請給予證明．
  【拓展應用】如圖3，直線y=ax-

  5

  a（a＜0）與x軸，y軸分別交于A、B兩點，分別以OB，AB為直角邊在第二、一象限內作等腰Rt△BOC和等腰Rt△BAD，連接CD，交y軸于點E．試猜想EB的長是否為定值，若是，請求出這個值；若不是，請說明理由．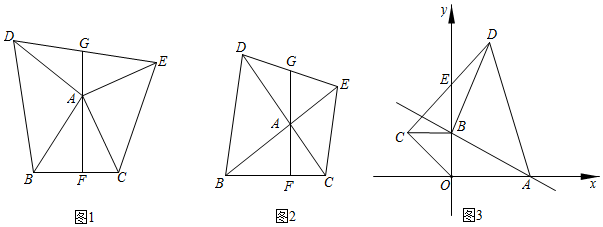
  
  組卷：801引用：4難度：0.3

  解析

• 25．如圖，已知二次函數y=ax²+bx+3的圖象與x軸分別交于A（1，0），B（3，0）兩點，與y軸交于點C
  
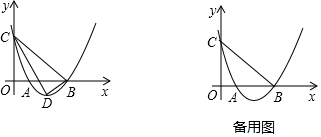
  （1）求此二次函數解析式；
  （2）點D為拋物線的頂點，試判斷△BCD的形狀，并說明理由；
  （3）將直線BC向上平移t（t＞0）個單位，平移后的直線與拋物線交于M，N兩點（點M在y軸的右側），當△AMN為直角三角形時，求t的值．
  組卷：2457引用：4難度：0.2

  解析