2022-2023學年陜西省安康市高二（下）期末數學試卷（理科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．復數

  z

  =

  -

  2

  i

  （

  -

  1

  +

  3

  i

  ）

  的虛部為（　　）

  A．-2

  B．2

  C．2i

  D． 2 3
  組卷：24引用：4難度：0.8

  解析

• 2．設全集U=R，集合A={x|x＜0}，B={x|（x+1）（x-2）＞0}，則?_U（A∪B）=（　　）

  A．（-∞，2]

  B．[0，+∞）

  C．[-1，2]

  D．[0，2]
  組卷：70引用：3難度：0.7

  解析

• 3．已知a=ln10，

  b

  =

  e

  ，c=2，則（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．c＞a＞b

  D．c＞b＞a
  組卷：109引用：4難度：0.7

  解析

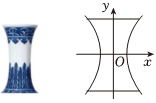• 4．如圖，這是一個落地青花瓷，其外形被稱為單葉雙曲面，可以看成是雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  的一部分繞其虛軸所在直線旋轉所形成的曲面．若該花瓶橫截面圓的最小直徑為8cm,瓶高等于雙曲線C的虛軸長，則該花瓶的瓶口直徑為（　　）

  A． 16 2 cm

  B．24cm

  C．32cm

  D． 8 2 cm
  組卷：167引用：8難度：0.5

  解析

• 5．執行如圖所示的程序框圖，則輸出的S=（　　）
  

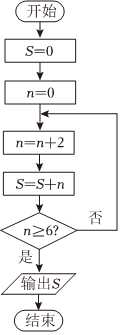
  A．6

  B．12

  C．20

  D．30
  組卷：2引用：3難度：0.8

  解析

• 6．將函數f（x）=sin（ωx+1）（ω＞0）的圖象向右平移1個單位長度后，得到的圖象關于原點對稱，則ω的最小值為（　　）

  A． 1 2

  B．1

  C．2

  D．4
  組卷：80引用：4難度：0.7

  解析

• 7．某校為了了解學生的身體素質，對2022屆初三年級所有學生仰臥起坐一分鐘的個數情況進行了數據統計，結果如圖所示．該校2023屆初三學生人數較2022屆初三學生人數上升了10%，則下列說法錯誤的是（　　）
  

  A．該校2022屆初三年級學生仰臥起坐一分鐘的個數在[30，60）內的學生人數占70%

  B．該校2023屆初三學生仰臥起坐一分鐘的個數在[60，80]內的學生人數比2022屆初三學生仰臥起坐一分鐘個數同個數段的學生人數的2倍還多

  C．該校2023屆初三學生仰臥起坐一分鐘的個數和2022屆初三學生仰臥起坐一分鐘個數的中位數均在[50，60）內

  D．相比2022屆初三學生仰臥起坐一分鐘個數不小于50的人數，2023屆初三學生仰臥起坐一分鐘個數不小于50的人數占比增加
  組卷：54引用：4難度：0.7

  解析

三、解答題：本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知拋物線C：y²=2px（p＞0）上一點M（1，m）（m＞0）與焦點的距離為2．
  （1）求p和m；
  （2）若在拋物線C上存在點A，B，使得MA⊥MB，設AB的中點為D，且D到拋物線C的準線的距離為

  15

  2

  ，求點D的坐標．
  組卷：135引用：6難度：0.4

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  x

  +

  a

  e

  x

  （

  a

  ∈

  R

  ）

  ．
  （1）討論f（x）的單調性；
  （2）若f（x）與函數g（x）=ae^x的圖象有三個不同的交點，求a的取值范圍．（參考數據：ln2≈0.7）
  組卷：47引用：4難度：0.6

  解析