2022-2023學年河南省信陽高級中學高二（上）期末數學試卷

一、選擇題（本大題共8小題，每題5分，共計40分．在每題給出的四個選項中，只有一個是正確的）

• 1．雙曲線

  x

  2

  3

  -

  y

  2

  2

  =1的漸近線方程是（　　）

  A．y= ± 6 2 x

  B．y= ± 6 3 x

  C．y= ± 3 2 x

  D．y= ± 2 3 x
  組卷：96引用：9難度：0.7

  解析

• 2．若平面α的法向量為

  μ

  ，直線l的方向向量為

  v

  ，直線l與平面α的夾角為θ，則下列關系式成立的是（　　）

  A．cosθ= u ? v | u | | v |

  B．cosθ= | u ? v | | u | | v |

  C．sinθ= u ? v | u | | v |

  D．sinθ= | u ? v | | u | | v |
  組卷：174引用：7難度：0.9

  解析

• 3．若拋物線C：x²=2py的焦點坐標為（0，1），則拋物線C的方程為（　　）

  A．x2=-2y

  B．x2=2y

  C．x2=-4y

  D．x2=4y
  組卷：30引用：2難度：0.9

  解析

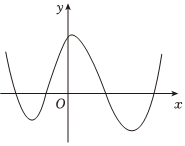• 4．函數f（x）的定義域為R，導函數f′（x）的圖象如圖所示，則函數f（x）（　　）

  A．無極大值點、有四個極小值點

  B．有三個極大值點、一個極小值點

  C．有兩個極大值點、兩個極小值點

  D．有四個極大值點、無極小值點
  組卷：98引用：5難度：0.5

  解析

• 5．已知點A（1，0），直線l：x-y+3=0，則點A到直線l的距離為（　　）

  A．1

  B．2

  C． 2

  D． 2 2
  組卷：919引用：3難度：0.9

  解析

• 6．已知A，B，C，D，E是空間中的五個點，其中點A，B，C不共線，則“存在實數x,y,使得

  DE

  =x

  AB

  +y

  AC

  是“DE∥平面ABC”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：341引用：10難度：0.8

  解析

• 7．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）與直線y=2x有交點，則雙曲線離心率的取值范圍為（　　）

  A．（1， 5 ）

  B．（1， 5 ]

  C．（ 5 ，+∞）

  D．[ 5 ，+∞）
  組卷：195引用：2難度：0.8

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數f（x）=ax-e^x（a∈R）．
  （1）求函數f（x）的單調區間；
  （2）設

  g

  （

  x

  ）

  =

  -

  3

  2

  x

  2

  +

  ax

  -

  1

  ，求證：當x∈[0，1]時，f（x）≤g（x）恒成立．
  組卷：353引用：3難度：0.4

  解析

• 22．已知橢圓C：

  x

  2

  4

  +

  y

  2

  =

  1

  的左右頂點分別為A₁，A₂，直線x=m（0＜m＜2）與C交于M、N兩點，直線A₁M和直線A₂N交于點P．
  （1）求P點的軌跡方程；
  （2）求

  |

  P

  A

  1

  |

  ?

  |

  PM

  |

  |

  P

  A

  2

  |

  ?

  |

  PN

  |

  的取值范圍．
  組卷：50引用：2難度：0.5

  解析