2023年四川省成都市郫都區高考數學段考試卷（理科）（三）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知復數z=a+i（a∈R），若z²=3+4i,則其共軛復數

  z

  在復平面內對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：126引用：2難度：0.8

  解析

• 2．某程序框圖如圖所示，則輸出的S=（　　）
  

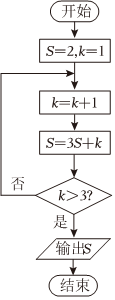
  A．8

  B．27

  C．85

  D．260
  組卷：64引用：6難度：0.8

  解析

• 3．設集合

  A

  =

  {

  x

  ∈

  N

  |

  8

  x

  +

  1

  ∈

  N

  }

  ，

  B

  =

  {

  x

  ∈

  N

  |

  x

  2

  -

  3

  x

  -

  4

  ≤

  0

  }

  ，則A∩B=（　　）

  A．{0，1，2}

  B．{0，1，3}

  C．{1，2，3}

  D．{1，2，4}
  組卷：140引用：4難度：0.7

  解析

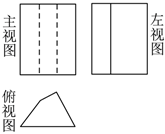• 4．一個幾何體的三視圖如圖所示，則這個幾何體是下面的（　　）

  A．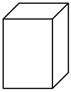

  B．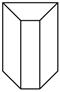

  C．

  D．
  組卷：48引用：3難度：0.7

  解析

• 5．若直線l：x+y+a=0是曲線C：y=x-2lnx的一條切線，則實數a的值為（　　）

  A．-3

  B．3

  C．-2

  D．2
  組卷：323引用：4難度：0.7

  解析

• 6．下列說法正確的有（　　）
  ①對于分類變量X與Y，它們的隨機變量K²的觀測值k越大，說明“X與Y有關系”的把握越大；
  ②我校高一、高二、高三共有學生4800人，其中高三有1200人．為調查需要，用分層抽樣的方法從全校學生中抽取一個容量為200的樣本，那么應從高三年級抽取40人；
  ③若數據x₁，x₂，…，x_n的方差為5，則另一組數據x₁+1，x₂+1，…，x_n+1的方差為6；
  ④把六進制數210_（6）轉換成十進制數為：210_（6）=0×6⁰+1×6¹+2×6²=78．

  A．①④

  B．①②

  C．③④

  D．①③
  組卷：103引用：3難度：0.7

  解析

• 7．程大位（1533～1606），明朝人，珠算發明家．在其杰作《直指算法統宗》里，有這樣一道題：蕩秋千，平地秋千未起，踏板一尺離地，送行二步與人齊，五尺人高曾記．仕女佳人爭蹴，終朝笑語歡嬉，良工高士素好奇，算出索長有幾？將其譯成現代漢語，其大意是，一架秋千當它靜止不動時，踏板離地一尺，將它向前推兩步（古人將一步算作五尺）即10尺，秋千的踏板就和人一樣高，此人身高5尺，如果這時秋千的繩索拉得很直，請問繩索有多長？（　　）

  A．14尺

  B．14.5尺

  C．15尺

  D．15.5尺
  組卷：96引用：4難度：0.8

  解析

選修4-4：坐標系與參數方程

• 22．已知在平面直角坐標系xOy中，直線l的參數方程為

  x = 3 + 2 t

  y = 3 - 2 3 t

  （t為參數），以坐標原點O為極點，x軸的正半軸為極軸，建立極坐標系，曲線C的極坐標方程為ρ（1+cos2θ）=2sinθ，點P的極坐標為

  （

  8

  ，

  2

  π

  3

  ）

  ．
  （1）求直線l的極坐標方程以及曲線C的直角坐標方程；
  （2）記M為直線l與曲線C的一個交點，其中|OM|＜4，求△OMP的面積．
  組卷：253引用：4難度：0.6

  解析

選修44-55：不等式選講

• 23．已知m≥0，函數f（x）=2|x-1|-|2x+m|的最大值為4，
  （1）求實數m的值；
  （2）若實數a,b,c滿足a-2b+c=m,求a²+b²+c²的最小值．
  組卷：32引用：5難度：0.7

  解析