2010年新課標七年級數學競賽培訓第26講：整數整除的概念與性質

一、填空題（共10小題，每小題4分，滿分40分）

• 1．一個自然數與13的和是5的倍數，與13的差是6的倍數，則滿足條件的最小自然數是

  ．
  組卷：180引用：1難度：0.9

  解析

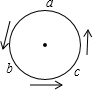• 2．如圖，若a、b、c是兩兩不等的非零數碼，按逆時針箭頭指向組成的兩位數

  ab

  、

  bc

  都是7的倍數，則可組成三位數

  abc

  共有

  個；其中最大的三位數與最小的三位數的和等于

  ．
  組卷：294引用：4難度：0.5

  解析

• 3．如果五位數

  12

  a

  34

  是3的倍數，那么a是

  ．
  組卷：89引用：1難度：0.7

  解析

• 4．如果從5，6，7，8，9這5個數中，選出4個組成一個四位數，使它能被3，5，7整除，那么這些數中最大的是

   

  ．
  組卷：91引用：1難度：0.9

  解析

• 5．已知整數

  13

  ab

  456

  能被198整除，那么a=

  ，b=

  ．
  組卷：132引用：2難度：0.5

  解析

• 6．在1，2，3，…，2000這2000個自然數中，有

  個自然數能同時被2和3整除，而且不能被5整除．
  組卷：340引用：3難度：0.3

  解析

• 7．五位數

  abcde

  是9的倍數，其中

  abcd

  是4的倍數，那么

  abcde

  的最小值是

  ．
  組卷：123引用：2難度：0.7

  解析

• 8．一個三位自然數，當它分別被2，3，4，5，7除時，余數都是1，那么具有這個性質的最小三位數是

   

  ；最大三位數是

   

  ．
  組卷：98引用：2難度：0.1

  解析

• 9．今天是星期日，從今天算起，第

  111

  …

  1

  2000

  個

  1

  天是星期

  ．
  組卷：163引用：4難度：0.7

  解析

• 10．用自然數n去除63、91、130，所得到的3個余數的和為26，則n=

  ．
  組卷：103引用：1難度：0.7

  解析

二、選擇題（共10小題，每小題3分，滿分30分）

• 11．有三個正整數a,b,c,其中a與b互質且b與c也互質．給出下面四個判斷：
  ①（a+c）²不能被b整除②a²+c²不能被b整除③（a+b）²不能被c整除④a²+b²不能被c整除
  其中，不正確的判斷有（　　）

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：148引用：2難度：0.9

  解析

• 12．盒中原有7個球，一位魔術師從中任取幾個球，把每一個小球都變成了7個小球，將其放回盒中，他又從盒中任取一些小球，把每一個小球又都變成了7個小球后放回盒中，如此進行，到某一時刻魔術師停止取球變魔術時，盒中球的總數可能是（　　）

  A．1990個

  B．1991個

  C．1992個

  D．1993個
  組卷：61引用：1難度：0.9

  解析

• 13．能整除任意3個連續整數之和的最大整數是（　　）

  A．1

  B．2

  C．3

  D．6
  組卷：328引用：6難度：0.9

  解析

三、解答題（共22小題，滿分110分）

• 40．任給一個自然數N，把N的各位數字按相反的順序寫出來，得到一個新的自然數N′，試證明：|N-N′|能被9整除．
  組卷：37引用：1難度：0.5

  解析

• 41．證明：111¹¹¹+112¹¹²+113¹¹³能被10整除．
  組卷：76引用：1難度：0.5

  解析