當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省廣州市越秀區(qū)育才實驗中學九年級（上）月考數(shù)學試卷（10月份）

發(fā)布：2024/4/20 14:35:0

一、選擇題

1．將方程3x²+1=6x化為一元二次方程的一般形式，其中二次項系數(shù)為3，則一次項系數(shù)、常數(shù)項分別是（　　）
A．-6、1 B．6、1 C．6、-1 D．-6、-1
組卷：179引用：18難度：0.9
解析
2．一元二次方程x²-4x+5=0的根的情況是（　　）
A．有兩個不相等的實數(shù)根 B．有兩個相等的實數(shù)根
C．只有一個實數(shù)根 D．沒有實數(shù)根
組卷：1752引用：160難度：0.9
解析
3．下列方程中，屬于一元二次方程是（　　）
A．2x²-y-1=0 B．x²=1
C．x²-x（x+7）=0 D．
1
x
2
=
1
組卷：937引用：12難度：0.9
解析
4．對于二次函數(shù)y=（x+2）²-3的圖象，下列說法正確的是（　　）
A．對稱軸是直線x=2 B．頂點坐標是（2，-3）
C．與x軸有兩個交點 D．開口向下
組卷：89引用：3難度：0.8
解析
5．將拋物線y=
1
2
x²向上平移2個單位長度，再向右平移3個單位長度后，得到的拋物線的解析式為（　　）
A．y=
1
2
（x-2）²+3 B．y=
1
2
（x+3）²+2
C．y=
1
2
（x-3）²+2 D．y=
1
2
（x+2）²+3
組卷：292引用：3難度：0.8
解析
6．拋物線y=x²-2x-1的圖象與x軸交點有（　　）
A．兩個交點 B．一個交點 C．無交點 D．無法確定
組卷：301引用：3難度：0.9
解析
7．用配方法解方程x²-2x-2=0，原方程應變形為（　　）
A．（x+1）²=3 B．（x-1）²=3 C．（x+1）²=1 D．（x-1）²=1
組卷：920引用：14難度：0.8
解析
8．若拋物線y=ax²+bx-3（a≠0）經(jīng)過點（-4，3）和點（8，3），則拋物線y=ax²+bx-3（a≠0）的對稱軸是直線（　　）
A．x=1 B．x=2 C．x=3 D．x=-1
組卷：654引用：4難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

三、解答題

24．使得函數(shù)值為零的自變量的值稱為函數(shù)的零點．例如，對于函數(shù)y=x-1，令y=0，可得x=1，我們就說1是函數(shù)y=x-1的零點．已知函數(shù)y=x²-2mx-2（m+3）（m為常數(shù)）．
（1）當m=0時，求該函數(shù)的零點；
（2）證明：無論m取何值，該函數(shù)總有兩個零點；
（3）設函數(shù)的兩個零點分別為x₁和x₂，且
1
x
1
+
1
x
2
=
-
1
4
，此時函數(shù)圖象與x軸的交點分別為A、B（點A在點B左側），點M在直線y=x-10上，當MA+MB最小時，求直線AM的函數(shù)解析式．
組卷：1255引用：18難度：0.5
解析
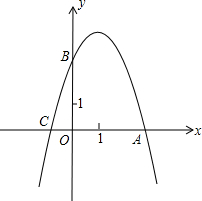25．已知拋物線y=ax²+2x+c的圖象與x軸交于點A（3，0）和點C，與y軸交于點B（0，3）．
（1）求拋物線的解析式；
（2）在拋物線的對稱軸上找一點D，使得點D到點B、C的距離之和最小，并求出點D的坐標；
（3）在第一象限的拋物線上，是否存在一點P，使得△ABP的面積最大？若存在，求出點P的坐標；若不存在，請說明理由．
組卷：717引用：12難度：0.5
解析