2023年安徽省江淮十校高考數(shù)學(xué)第四次聯(lián)考試卷

一、單項選擇題：本題共8小題．每小題5分，共40分．在每小題給出的四個選項中，只有一項符合題目要求．

• 1．已知集合A={（x,y）|y=x²}，集合B={（x,y）|y=1-|x|}，則集合A∩B的元素個數(shù)為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：108引用：5難度：0.7

  解析

• 2．已知直線l的一個方向向量為

  p

  =

  （

  sin

  π

  3

  ，

  cos

  π

  3

  ）

  ，則直線l的傾斜角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 4 π 3
  組卷：637引用：7難度：0.8

  解析

• 3．已知a,b為實數(shù)，則使得“a＞b＞0”成立的一個充分不必要條件為（　　）

  A． 1 a ＞ 1 b	B．ln（a+1）＞ln（b+1）
  C．a(chǎn)3＞b3	D． a - 1 ＞ b - 1
  組卷：347引用：7難度：0.6

  解析

• 4．“學(xué)如逆水行舟，不進(jìn)則退；心似平原跑馬，易放難收”（明?《增廣賢文》）是勉勵人們專心學(xué)習(xí)的．如果每天的“進(jìn)步”率都是1%，那么一年后是（1+1%）³⁶⁵=1.01³⁶⁵；如果每天的“退步”率都是1%，那么一年后是（1-1%）³⁶⁵=0.99³⁶⁵.一年后“進(jìn)步”的是“退步”的

  1

  .

  01

  365

  0

  .

  99

  365

  =

  （

  1

  .

  01

  0

  .

  99

  ）

  365

  ≈

  1481

  倍．如果每月的“進(jìn)步”率和“退步”率都是20%，那么大約經(jīng)過（　　）月后“進(jìn)步”的是“退步”的一萬倍．（lg2≈0.3010，lg3≈0.4771）

  A．20

  B．21

  C．22

  D．23
  組卷：309引用：9難度：0.8

  解析

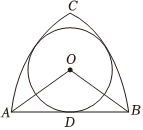• 5．哥特式建筑是1140年左右產(chǎn)生于法國的歐洲建筑風(fēng)格，它的特點(diǎn)是尖塔高聳、尖形拱門、大窗戶及繪有故事的花窗玻璃，如圖所示的幾何圖形，在哥特式建筑的尖形拱門與大窗戶中較為常見，它是由線段AB和兩個圓弧AC、BC圍成，其中一個圓弧的圓心為A，另一個圓弧的圓心為B，圓O與線段AB及兩個圓弧均相切，若AB=2，則

  OA

  ?

  OB

  =（　　）

  A． - 7 16

  B． - 2 7

  C． - 4 3

  D． - 4 7
  組卷：141引用：5難度：0.4

  解析

• 6．將函數(shù)

  f

  （

  x

  ）

  =

  sin

  （

  x

  +

  π

  3

  ）

  +

  sinx

  的圖像向左平移a（a＞0）個單位后的函數(shù)圖像關(guān)于y軸對稱，則實數(shù)a的最小值為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 2
  組卷：164引用：4難度：0.6

  解析

• 7．若（mx-1）ⁿ（n∈N^*）的展開式中，所有項的系數(shù)和與二項式系數(shù)和相等，且第6項的二項式系數(shù)最大，則有序?qū)崝?shù)對（m,n）共有（　　）組不同的解．

  A．1

  B．2

  C．3

  D．4
  組卷：239引用：7難度：0.8

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．

• 21．已知點(diǎn)F（0，1），動點(diǎn)M在直線l：y=-1上，過點(diǎn)M且垂直于x軸的直線與線段MF的垂直平分線交于點(diǎn)P，記點(diǎn)P的軌跡為曲線C．
  （1）求曲線C的標(biāo)準(zhǔn)方程；
  （2）過F的直線與曲線C交于A，B兩點(diǎn)，直線OA，OB與圓x²+y²-2y=0的另一個交點(diǎn)分別為D，E，求△DOE與△AOB面積之比的最大值．
  組卷：243引用：7難度：0.3

  解析

• 22．對于定義在D上的函數(shù)F（x），若存在x₀∈D，使得F（x₀）=x₀，則稱x₀為F（x）的一個不動點(diǎn)．設(shè)函數(shù)f（x）=（x-1）e^x-alnx+x,已知x₀（x₀≠1）為函數(shù)f（x）的不動點(diǎn)．
  （1）求實數(shù)a的取值范圍；
  （2）若k∈Z，且kx₀＜a對任意滿足條件的x₀成立，求整數(shù)k的最大值．
  （參考數(shù)據(jù)：ln2≈0.693，ln3≈1.1，

  e

  2

  3

  ≈

  1

  .

  95

  ，e²≈7.39，

  e

  3

  2

  ≈

  4

  .

  48

  ）
  組卷：142引用：4難度：0.1

  解析