2022-2023學年浙江省寧波市余姚市姚江教共體九年級（上）第一次聯考數學試卷

一、選擇題（每題4分，共40分）

• 1．一個袋子中有7只黑球，6只黃球，5只白球，一次性取出12只球，其中出現黑球是（　　）

  A．不可能事件	B．必然事件
  C．隨機事件	D．以上說法均不對
  組卷：30引用：3難度：0.9

  解析

• 2．⊙O內有一點P，過點P的所有弦中，最長的為10，最短的為8，則OP的長為（　　）

  A．6

  B．5

  C．4

  D．3
  組卷：108引用：2難度：0.7

  解析

• 3．已知點A（1，y₁），B（2

  2

  ，y₂），C（4，y₃）在二次函數y=x²-6x+c的圖象上，則y₁，y₂，y₃的大小關系是（　　）

  A．y1＜y2＜y 3

  B．y2＜y3＜y 1

  C．y3＜y2＜y1

  D．y1＜y3＜y2
  組卷：637引用：3難度：0.5

  解析

• 4．已知實數a,b,c滿足：a＜0，a-b+c＞0，則一定有（　　）

  A．b2-4ac＞0

  B．b2-4ac≥0

  C．b2-4ac≤0

  D．b2-4ac＜0
  組卷：460引用：16難度：0.7

  解析

• 5．小明利用測角儀和旗桿的拉繩測量學校旗桿的高度．如圖，旗桿PA的高度與拉繩PB的長度相等．小明將PB拉到PB′的位置，測得∠PB′C=α（B′C為水平線），測角儀B′D的高度為1米，則旗桿PA的高度為（　　）

  A． 1 1 - sinα

  B． 1 1 + sinα

  C． 1 1 - cosα

  D． 1 1 + cosα
  組卷：3253引用：28難度：0.7

  解析

• 6．如圖，將一張直角三角形紙片沿虛線剪成甲、乙、丙三塊，其中甲、丙為梯形，乙為三角形．根據圖中標示的邊長數據，比較甲、乙、丙的面積大小，下列判斷何者正確？（　　）
  

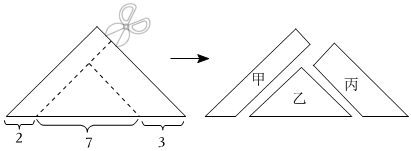
  A．甲＞乙，乙＞丙	B．甲＞乙，乙＜丙
  C．甲＜乙，乙＞丙	D．甲＜乙，乙＜丙
  組卷：419引用：63難度：0.5

  解析

• 7．如圖，△ABC中，∠A、∠B、∠C所對的三邊分別記為a,b,c,O是△ABC的外心，OD⊥BC，OE⊥AC，OF⊥AB，則OD：OE：OF=（　　）

  A．a：b：c	B． 1 a ： 1 b ： 1 c
  C．cosA：cosB：cosC	D．sinA：sinB：sinC
  組卷：1168引用：16難度：0.9

  解析

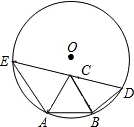• 8．已知AB是半徑為1的圓O的一條弦，且AB=a＜1，以AB為一邊在圓O內作正△ABC，點D為圓O上不同于點A的一點，且DB=AB=a,DC的延長線交圓O于點E，則AE的長為（　　）

  A． 5 2 a

  B．1

  C． 3 2

  D．a
  組卷：2693引用：23難度：0.5

  解析

三、解答題（本大題有8小題，共80分）

• 23．如圖，在平面直角坐標系中，拋物線

  y

  =

  1

  4

  x

  2

  -

  3

  2

  x

  -

  4

  ，y與x軸交于A，B兩點，與y軸交于點C．
  （1）直接寫出點A、B、C的坐標；
  （2）直接寫出△ABC的重心點M的坐標；
  （3）坐標系中存在點N（n,6），且∠ANB=45°，請你推導計算出n的值；
  （4）如圖2．若點P在以點O為圓心，OA長為半徑作的圓上，連接BP、CP，請你直接寫出

  1

  2

  CP

  +

  BP

  的最小值．
  組卷：39引用：2難度：0.5

  解析

• 24．對于半徑為r的⊙P及一個正方形給出如下定義：若⊙P上存在到此正方形四條邊距離都相等的點，則稱⊙P是該正方形的“等距圓”．如圖1，在平面直角坐標系xOy中，正方形ABCD的頂點A的坐標為（2，4），頂點C、D在x軸上，且點C在點D的左側．
  （1）當r=4

  2

  時，
  ①在P₁（0，-3），P₂（4，6），P₃（4

  2

  ，2）中可以成為正方形ABCD的“等距圓”的圓心的是

  ；
  ②若點P在直線y=-x+2上，且⊙P是正方形ABCD的“等距圓”，則點P的坐標為

  ；
  （2）如圖2，在正方形ABCD所在平面直角坐標系xOy中，正方形EFGH的頂點F的坐標為（6，2），頂點E、H在y軸上，且點H在點E的上方．
  ①若⊙P同時為上述兩個正方形的“等距圓”，且與BC所在直線相切，求⊙P在y軸上截得的弦長；
  ②將正方形ABCD繞著點D旋轉一周，在旋轉的過程中，線段HF上沒有一個點能成為它的“等距圓”的圓心，則r的取值范圍是

  ．
  
  組卷：160引用：2難度：0.3

  解析