2022-2023學年新疆克孜勒蘇柯爾克孜一中高三（上）期中數學試卷（文科）

一、選擇題；本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知p：a＞b＞0，q：

  1

  a

  2

  ＜

  1

  b

  2

  ，則p是q的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：614引用：12難度：0.8

  解析

• 2．已知集合A={x|2x²+7x-4＜0}，B={x|

  （

  1

  2

  ）

  -

  x

  ≥

  1

  8

  }，則A∩B=（　　）

  A．{x|-3＜x＜ 1 2 }

  B．{x|-3≤x＜ 1 2 }

  C．{x|-4≤x＜-3}

  D．{x|- 1 2 ≤x＜3}
  組卷：253引用：3難度：0.7

  解析

• 3．若直線ax+y+1=0與x+（2a+1）y+2=0平行，則a的值為（　　）

  A． 1 2

  B．-1

  C． 1 2 或-1

  D．- 1 2 或1
  組卷：384引用：5難度：0.7

  解析

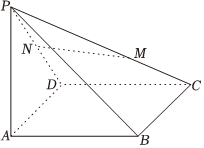• 4．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，M，N分別為PC，PD上的點，且

  PM

  =

  2

  MC

  ，

  PN

  =

  ND

  ，若

  NM

  =

  x

  AB

  +

  y

  AD

  +

  z

  AP

  ，則x+y+z的值為（　　）

  A． - 2 3

  B． 2 3

  C．1

  D． 5 6
  組卷：137引用：3難度：0.8

  解析

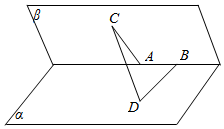• 5．如圖所示，已知在一個60°的二面角的棱上，有兩個點A，B，AC，BD分別是在這個二面角的兩個面內垂直于AB的線段，且AB=4cm,AC=6cm,BD=8cm,則CD的長為（　　）

  A．2 17

  B．2 41

  C．2

  D．10
  組卷：132引用：5難度：0.9

  解析

• 6．過點A（1，2）且與原點距離最大的直線方程為（　　）

  A．2x+y-4=0

  B．x+2y-5=0

  C．x+3y-7=0

  D．3x+y-5=0
  組卷：1397引用：25難度：0.9

  解析

• 7．三棱錐S-ABC中，SA⊥底面ABC，SA=4，AB=3，D為AB的中點，∠ABC=90°，則點D到面SBC的距離等于（　　）

  A． 12 5

  B． 9 5

  C． 6 5

  D． 3 5
  組卷：239引用：3難度：0.5

  解析

三、解答題；本題共6個小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

• 21．某地區上年度電價為0.8元/kW?h,年用電量為akW?h,本年度計劃將電價降到0.55元/kW?h至0.75元/kW?h之間，而用戶期望電價為0.4元/kW?h經測算，下調電價后新增的用電量與實際電價和用戶期望電價的差成反比（比例系數為k）．該地區電力的成本為0.3元/kW?h.
  （1）寫出本年度電價下調后，電力部門的收益y與實際電價x的函數關系式；
  （2）設k=0.2a,當電價最低定為多少時仍可保證電力部門的收益比上年至少增長20%？
  （注：收益=實際用電量×（實際電價-成本價））
  組卷：990引用：27難度：0.1

  解析

• 22．已知定義域為R的函數

  f

  （

  x

  ）

  =

  b

  x

  +

  n

  -

  2

  b

  x

  -

  2

  是奇函數，且指數函數y=b^x的圖象過點（2，4）．
  （1）求f（x）的表達式；
  （2）若方程f（x²+3x）+f（-a+x）=0，x∈（-4，+∞）恰有2個互異的實數根，求實數a的取值集合；
  （3）若對任意的t∈[-1，1]，不等式f（t²-2a）+f（at-1）≥0恒成立，求實數a的取值范圍．
  組卷：182引用：4難度：0.5

  解析