2020-2021學(xué)年吉林省長春市榆樹高級中學(xué)高二（下）期中數(shù)學(xué)試卷（文科）

一、選擇題：（每小題5分，共計60分）

• 1．復(fù)數(shù)z=

  1

  +

  2

  i

  1

  -

  i

  ，則

  z

  =（　　）

  A． 1 2 - 3 2 i

  B． - 1 2 - 3 2 i

  C． 1 2 + 3 2 i

  D． - 1 2 + 3 2 i
  組卷：89引用：2難度：0.8

  解析

• 2．演繹推理“因為對數(shù)函數(shù)y=log_ax（a＞0且a≠1）是增函數(shù)，而函數(shù)y=lo

  g

  1

  2

  x是對數(shù)函數(shù)，所以y=lo

  g

  1

  2

  x是增函數(shù)”所得結(jié)論錯誤的原因是（　　）

  A．推理形式錯誤	B．小前提錯誤
  C．大前提錯誤	D．大前提和小前提都錯誤
  組卷：65引用：20難度：0.9

  解析

• 3．如表為某班5位同學(xué)身高x（單位：cm）與體重y（單位kg）的數(shù)據(jù)，
  

  身高	170	171	166	178	160
  體重	75	80	70	85	65

  若兩個量間的回歸直線方程為

  ?

  y

  =1.16x+a,則a的值為（　　）

  A．-122.2

  B．-121.04

  C．-91

  D．-92.3
  組卷：62引用：7難度：0.9

  解析

• 4．若曲線

  x = 2 - tsin 30 °

  y = - 1 + tsin 30 °

  （t為參數(shù)）與曲線ρ=2

  2

  相交于B，C兩點，則|BC|的值為（　　）

  A．2 7

  B． 60

  C．7 2

  D． 30
  組卷：400引用：11難度：0.9

  解析

• 5．曲線的極坐標(biāo)方程ρ=4sinθ化為直角坐標(biāo)為（　　）

  A．x2+（y+2）2=4	B．x2+（y-2）2=4
  C．（x-2）2+y2=4	D．（x+2）2+y2=4
  組卷：1686引用：71難度：0.9

  解析

• 6．如圖，在復(fù)平面內(nèi)，點A表示復(fù)數(shù)z,則圖中表示z的共軛復(fù)數(shù)的點是（　　）
  

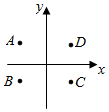
  A．A

  B．B

  C．C

  D．D
  組卷：63引用：5難度：0.9

  解析

• 7．復(fù)數(shù)

  1

  +

  i

  1

  -

  i

  =（　　）

  A．-i

  B．-1

  C．i

  D．1
  組卷：54引用：20難度：0.9

  解析

三、解答題長.

• 21．已知直線l₁過點P（1，-1），傾斜角為

  π

  4

  ，
  （1）求直線l₁的參數(shù)方程；
  （2）設(shè)直線l₂的方程為x+y-3=0，l₁與l₂的交點為Q，求|PQ|的長．
  組卷：44引用：1難度：0.5

  解析

• 22．在直角坐標(biāo)系xOy中，直線l的參數(shù)方程為

  x = - 5 + 2 2 t

  y = 5 + 2 2 t

  （t為參數(shù)）若以O(shè)點為極點，x軸正半軸為極軸建立極坐標(biāo)系，則曲線C的極坐標(biāo)方程為ρ=4cosθ．
  （1）求曲線C的直角坐標(biāo)方程及直線l的普通方程；
  （2）將曲線C上各點的橫坐標(biāo)縮短為原來的

  1

  2

  ，再將所得曲線向左平移1個單位，得到曲線C₁，求曲線C₁上的點到直線l的距離的最小值．
  組卷：821引用：19難度：0.5

  解析