2023-2024學年江蘇省無錫市江陰市澄西片八年級（上）期中數學試卷

一、選擇題（本大題共10小題，每小題3分，共30分.）

• 1．下面四個圖形分別是不可回收垃圾、可回收垃圾、有害垃圾、其它垃圾的標志，這四個標志中是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：529引用：27難度：0.9

  解析

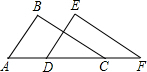• 2．如圖，點A，D，C，F在一條直線上，AB=DE，∠A=∠EDF，補充下列條件不能證明△ABC≌△DEF的是（　　）

  A．AD=CF

  B．BC∥EF

  C．∠B=∠E

  D．BC=EF
  組卷：802引用：4難度：0.9

  解析

• 3．等腰三角形的兩條邊長分別為2和4，則這個等腰三角形的周長為（　　）

  A．8或10

  B．8

  C．10

  D．11
  組卷：131引用：4難度：0.6

  解析

• 4．下列實數中，無理數的是（　　）

  A．0

  B． 4

  C． 1 3

  D．-π
  組卷：107引用：3難度：0.7

  解析

• 5．下列各組數中能作為直角三角形的三邊長的是（　　）

  A．4，5，6

  B．1，1， 2

  C．6，8，11

  D．5，12，23
  組卷：222引用：27難度：0.9

  解析

• 6．已知實數

  a

  =

  13

  ，a介于兩個連續自然數之間，則下列正確的是（　　）

  A．1＜a＜2

  B．2＜a＜3

  C．3＜a＜4

  D．4＜a＜5
  組卷：85引用：2難度：0.9

  解析

• 7．如圖，在△ABC中，AB=AC=5，BC=8，D是線段BC上（不含端點B，C）的動點．若線段AD長為正整數，則點D的個數共有（　　）

  A．5個

  B．3個

  C．2個

  D．1個
  組卷：852引用：5難度：0.5

  解析

• 8．近似數3.45萬精確到哪一位（　　）

  A．百分位

  B．十分位

  C．百位

  D．萬位
  組卷：121引用：2難度：0.7

  解析

三、解答題（本大題共8小題，共65分.解答時應寫出文字說明、證明過程或演算步驟）

• 25．如田是由邊長為1的小正方形構成的網格，每個小正方形的頂點叫做格點，△ABC的頂點在格點上，僅用無刻度尺的直尺在給定網格中畫圖，畫圖過程用虛線表示，畫圖結果用實線表示，按步驟完成下列問題：
  （1）AC的長為

  ；
  （2）△BAC的面積

  ；
  （3）利用網格畫△BAC的角平分線AD；
  （4）E是AC與網格線的交點，請在AD上找一個點Q，使得QC+QE最小．
  組卷：173引用：1難度：0.5

  解析

• 26．【情境建模】（1）蘇科版教材八年級上冊第60頁，研究了等腰三角形的軸對稱性，我們知道“等腰三角形底邊上的高線、中線和頂角平分線重合”，簡稱“三線合一”．
  小明嘗試著逆向思考：若三角形一個角的平分線與這個角對邊上的高重合，則這個三角形是等腰三角形．如圖1，已知，點D在△ABC的邊BC上，AD平分∠BAC，且AD⊥BC，求證：AB=AC．請你幫助小明完成證明．
  請嘗試直接應用“情境建模”中小明反思出的結論解決下列問題：
  【理解內化】（2）①如圖2，在△ABC中，AD是角平分線，過點B作AD的垂線交AD、AC于點E、F，∠ABF=2∠C，求證：

  BE

  =

  1

  2

  （

  AC

  -

  AB

  ）

  ．
  ②如圖3，在四邊形ABDC中，

  BC

  =

  7

  ，

  AC

  -

  AB

  =

  2

  ，AD平分∠CAB，AD⊥CD，當△BCD的面積最大時，請直接寫出此時CD的長．
  【拓展應用】（3）如圖4，△ABC是兩條公路岔路口綠化施工的一塊區域示意圖，其中∠ACB=90°，AC=15m,BC=20m,該綠化帶中修建了健身步道．OA、OB、OM、ON、MN，其中入口M、N分別在AC、BC上，步道OA、OB分別平分∠BAC和∠ABC，OM⊥OA，ON⊥OB．現要用圍擋完全封閉△CMN區域，修建地下排水和地上公益廣告等設施，請直接寫出圍擋的長度．（步道寬度和接頭忽略不計）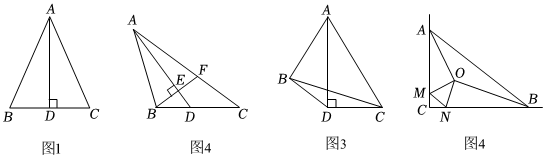
  
  組卷：341引用：1難度：0.5

  解析