2022-2023學年上海市寶山區行知中學高二（下）月考數學試卷（5月份）

一、填空題（第1-6題每題4分，第7-12題每題5分，滿分48分）

• 1．拋物線的標準方程為y²=4x,則它的準線方程為

   

  ．
  組卷：22引用：2難度：0.5

  解析

• 2．已知數列{a_n}的通項公式為

  a

  n

  =

  2 n , n = 1 ，

  2 - n ， n ≥ 2 ，

  前n項和為S_n，則

  lim

  n

  →

  +

  ∞

  S

  n

  =

  ．
  組卷：181引用：4難度：0.6

  解析

• 3．已知直線l的方程為

  x

  2

  +

  y

  2

  =

  1

  ，則直線l的傾斜角α=

  ．
  組卷：315引用：5難度：0.9

  解析

• 4．數列{a_n}的通項公式為

  a

  n

  =

  （

  -

  1

  ）

  n

  （

  2

  n

  +

  1

  ）

  （

  n

  ∈

  N

  *

  ）

  ，

  S

  n

  是其前n項和，則S₁₅=

  ．
  組卷：85引用：4難度：0.6

  解析

• 5．已知數列{a_n}的前n項和為S_n，若

  S

  n

  =

  3

  2

  n

  2

  -

  4

  n

  ，則a₆=

  ．
  組卷：22引用：2難度：0.7

  解析

• 6．若圓（x-1）²+y²=4與直線x+y+1=0相交于A，B兩點，則弦|AB|的長為

   

  ．
  組卷：96引用：10難度：0.7

  解析

• 7．在長方體ABCD-A₁B₁C₁D₁中，AD=AA₁=1，AB=2，若E為AB的中點，則點E到面ACD₁的距離是

  ．
  組卷：213引用：11難度：0.7

  解析

三、解答題（本大題共有5題，滿分0分）

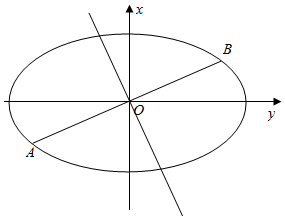• 20．在平面直角坐標系xoy中，已知橢圓C的方程為

  x

  2

  8

  +y²=1，設AB是過橢圓C中心O的任意弦，l是線段AB的垂直平分線，M是l上與O不重合的點．
  （1）求以橢圓的焦點為頂點，頂點為焦點的雙曲線方程；
  （2）若MO=2OA，當點A在橢圓C上運動時，求點M的軌跡方程；
  （3）記M是l與橢圓C的交點，若直線AB的方程為y=kx（k＞0），當△AMB面積取最小值時，求直線AB的方程．
  組卷：123引用：4難度：0.3

  解析

• 21．設{a_n}是公差不為零的等差數列，滿足a₁=1，a₆+a₇=a₁₃，設正項數列{b_n}的前n項和為S_n，且4S_n+2b_n=3．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）在b₁和b₂之間插入1個數x₁₁，使b₁、x₁₁、b₂成等差數列；在b₂和b₃之間插入2個數x₂₁、x₂₂，使b₂、x₂₁、x₂₂、b₃成等差數列；…；在b_n和b_n+1之間插入n個數x_n1、x_n2、…、x_nn，使b_n、x_n1、x_n2、…、x_nn、b_n+1成等差數列，求T_n=x₁₁+x₂₁+x₂₂+…+x_n1+x_n2+…+x_nn；
  （3）對于（2）中求得的T_n，是否存在正整數m、n,使得

  T

  n

  =

  a

  m

  +

  1

  2

  a

  m

  成立？若存在，求出所有的正整數對（m,n）；若不存在，請說明理由．
  組卷：231引用：4難度：0.2

  解析