2022-2023學(xué)年江西省新余市高一（上）期末數(shù)學(xué)試卷
發(fā)布：2024/4/20 14:35:0
一、單選題（本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的）
-
1．命題“?x0∈（0，+∞），lnx0=x0-1”的否定是（ ）
組卷：4921引用：126難度：0.9 -
2．已知集合A={x|x2-1≤0，x∈Z}，B={-2，-1，0，1，2}，則A∩B子集的個(gè)數(shù)為（ ）
組卷：850引用：6難度：0.9 -
3．某工廠利用隨機(jī)數(shù)表對生產(chǎn)的600個(gè)零件進(jìn)行抽樣測試，先將600個(gè)零件進(jìn)行編號，編號分別為001，002，…，599，600．從中抽取60個(gè)樣本，如下提供隨機(jī)數(shù)表的第4行到第6行：
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若從表中第6行第6列開始向右讀取數(shù)據(jù)，則得到的第6個(gè)樣本編號是（ ）組卷：516引用：3難度：0.9 -
4．若函數(shù)f（x）=
（a＞0，a≠1）是R上的單調(diào)函數(shù)，則a的取值范圍為（ ）ax-3，x≥4，-ax+4，x＜4組卷：195引用：4難度：0.7 -
5．“不積跬步，無以至千里：不積小流，無以成江海．”，每天進(jìn)步一點(diǎn)點(diǎn)，前進(jìn)不止一小點(diǎn)．今日距離高考還有936天，我們可以把（1+1%）936看作是每天的“進(jìn)步”率都是1%，高考時(shí)是1.01936≈11086.79；而把（1-1%）936看作是每天“退步”率都是1%．高考時(shí)是0.99936≈0.000082．若“進(jìn)步”的值是“退步”的值的100倍，大約經(jīng)過（ ）天（參考數(shù)據(jù)：lg101≈2.0043，lg99≈1.9956）
組卷：163引用：8難度：0.7 -
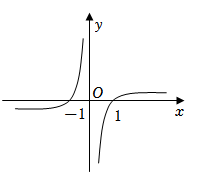6．已知函數(shù)f（x）的圖象如圖所示，那么該函數(shù)可能為（ ）組卷：151引用：3難度：0.7 -
7．已知a,b∈R，且a≠b,滿足
，若對于任意的x∈[3，6]，均有tx2+2x≤a+b成立，則實(shí)數(shù)t的最大值是（ ）（a-2）4+（a-2）2=2022（b-2）4+（b-2）2=2022組卷：23引用：1難度：0.6
四、解答題（本大題共6小題，17題10分，18～22題各12分，共70分．解答須寫出文字說明、證明過程和演算步驟）
-
21．小李同學(xué)大學(xué)畢業(yè)后，決定利用所學(xué)專業(yè)進(jìn)行自主創(chuàng)業(yè)．經(jīng)過調(diào)查，生產(chǎn)某小型電子產(chǎn)品需投入年固定成本5萬元，每年生產(chǎn)x萬件，需另投入流動(dòng)成本C（x）萬元，在年產(chǎn)量不足8萬件時(shí)，
（萬元）；在年產(chǎn)量不小于8萬件時(shí)，C（x）=12x2+4x（萬元），每件產(chǎn)品售價(jià)為10元，經(jīng)分析，生產(chǎn)的產(chǎn)品當(dāng)年能全部售完．C（x）=11x+49x-33
（1）寫出年利潤P（x）（萬元）關(guān)于年產(chǎn)量x（萬件）的函數(shù)解析式；
（年利潤=年銷售收入-固定成本-流動(dòng)成本）
（2）年產(chǎn)量為多少萬件時(shí)，小李在這一產(chǎn)品的生產(chǎn)中所獲利潤最大？最大利潤是多少？組卷：154引用：4難度：0.5 -
22．已知
，g（x）=ln[（3-a）ex+1]-ln3a-2x.f（x）=ex+k?1ex
（1）若函數(shù)f（x）在[0，+∞）為增函數(shù)，求實(shí)數(shù)k的取值范圍；
（2）若函數(shù)f（x）為偶函數(shù)，對于任意x1∈[0，+∞），任意x2∈R，使得g（x1）≤f（x2）-2成立，求a的取值范圍．組卷：71引用：3難度：0.3