2022-2023學年上海市浦東新區建平中學高三（上）月考數學試卷（11月份）

一、填空題（本大題共有12小題，滿分54分，第1-6題每題4分，第7-12題每題5分）

• 1．已知集合M={x|-4＜x＜3}，N={-4，-2，1，2}，則?_R（M∪N）=

  ．
  組卷：104引用：2難度：0.8

  解析

• 2．已知復數

  z

  =

  2

  -

  i

  （

  -

  1

  +

  i

  ）

  2

  ，則

  z

  =

  ．
  組卷：76引用：2難度：0.8

  解析

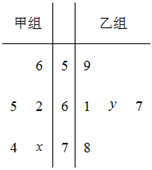• 3．如圖所示的莖葉圖記錄了甲、乙兩組各5名工人某日的產量數據（單位：件）．若這兩組數據的中位數相等，且平均值也相等，則x和y的值分別為

  ．
  組卷：34引用：2難度：0.8

  解析

• 4．已知

  （

  x

  2

  -

  1

  x

  ）

  n

  的展開式中，若第7項為常數項，則n的值為

  ．
  組卷：45引用：2難度：0.7

  解析

• 5．已知函數

  f

  （

  x

  ）

  =

  3

  sinωx

  +

  cosωx

  （

  ω

  ＞

  0

  ）

  的圖像與直線y=2的兩個相鄰交點的距離等于π，則ω的值為

  ．
  組卷：91引用：1難度：0.7

  解析

• 6．設F₁和F₂為雙曲線4x²-2y²=1的兩個焦點，點P在雙曲線上，且滿足∠F₁PF₂=60°，則△F₁PF₂的面積是
  組卷：193引用：5難度：0.7

  解析

• 7．若非零數a,b滿足3a=2b（a+1），且直線

  2

  x

  a

  +

  y

  2

  b

  =1恒過一定點，則定點坐標為

   

  ．
  組卷：83引用：2難度：0.9

  解析

三、解答題（本大題共5題，滿分76分）

• 20．已知二次曲線C_k的方程：

  x

  2

  9

  -

  k

  +

  y

  2

  4

  -

  k

  =

  1

  ．
  （1）分別求出方程表示橢圓和雙曲線的條件；
  （2）若雙曲線C_k與直線y=x+1有公共點且實軸最長，求雙曲線方程；
  （3）m、n為正整數，且m＜n,是否存在兩條曲線C_m，C_n，其交點P與點

  F

  1

  （

  -

  5

  ，

  0

  ）

  ，

  F

  2

  （

  5

  ，

  0

  ）

  滿足

  P

  F

  1

  ?

  P

  F

  2

  =

  0

  ？若存在，求m、n的值；若不存在，說明理由．
  組卷：70引用：3難度：0.7

  解析

• 21．設函數f（x）=（x-t₁）（x-t₂）（x-t₃），其中t₁，t₂，t₃∈R，且t₁，t₂，t₃是公差為d的等差數列．
  （Ⅰ）若t₂=0，d=1，求曲線y=f（x）在點（0，f（0））處的切線方程；
  （Ⅱ）若d=3，求f（x）的極值；
  （Ⅲ）若曲線y=f（x）與直線y=-（x-t₂）-6

  3

  有三個互異的公共點，求d的取值范圍．
  組卷：2121引用：2難度：0.1

  解析