當前位置：試卷中心 > 試卷詳情

《第9章平面向量》2013年單元測試卷

發布：2024/12/12 6:30:2

一、選擇題

1．設
a
、
b
、
c
是單位向量，且
a
?
b
=
0
，則
（
a
-
c
）
?
（
b
-
c
）
的最小值為（　　）
A．-2 B．
2
-2 C．-1 D．1-
2
組卷：1810引用：34難度：0.9
解析
2．已知向量
a
=（2，1），
a
?
b
=10，|
a
+
b
|=
5
2
，則|
b
|=（　　）
A．
5
B．
10
C．5 D．25
組卷：5324引用：104難度：0.9
解析
3．平面向量
a
與
b
的夾角為60°，
a
=（2，0），|
b
|=1，則|
a
+2
b
|=（　　）
A．
3
B．
2
3
C．4 D．12
組卷：2683引用：146難度：0.9
解析
4．在△ABC中，M是BC的中點，AM=1，點P在AM上且滿足
PA
=
-
2
PM
，則
PA
?
（
PB
+
PC
）
等于（　　）
A．
4
9
B．
4
3
C．
-
4
3
D．
-
4
9
組卷：266引用：8難度：0.9
解析
5．已知向量
a
=（-3，2），
b
=（-1，0），若λ
a
+
b
與
a
-2
b
垂直，則實數λ的值為（　　）
A．-
1
7
B．
1
7
C．-
1
6
D．
1
6
組卷：463引用：21難度：0.9
解析
6．設D、E、F分別是△ABC的三邊BC、CA、AB上的點，且
DC
=
2
BD
，
CE
=
2
EA
，
AF
=
2
FB
，則
AD
+
BE
+
CF
與
BC
（　　）
A．反向平行 B．同向平行
C．互相垂直 D．既不平行也不垂直
組卷：1001引用：19難度：0.9
解析
7．已知
a
，
b
是平面內兩個互相垂直的單位向量，若向量
c
滿足（
a
-
c
）?（
b
-
c
）=0，則|
c
|的最大值是（　　）
A．1 B．2 C．
2
D．
2
2
組卷：1911引用：20難度：0.9
解析
8．已知O是△ABC所在平面內一點，D為BC邊中點，且
2
OA
+
OB
+
OC
=
0
，那么（　　）
A．
AO
=
OD
B．
AO
=
2
OD
C．
AO
=
3
OD
D．
2
AO
=
OD
組卷：2795引用：72難度：0.9
解析
9．設
a
=
（
4
，
3
）
，
a
在
b
上的投影為
5
2
2
，
b
在x軸上的投影為2，且
|
b
|
≤
14
，則
b
為（　　）
A．（2，14） B．
（
2
，-
2
7
）
C．
（
-
2
，
2
7
）
D．（2，8）
組卷：809引用：13難度：0.9
解析
10．設
a
，
b
是非零向量，若函數
f
（
x
）
=
（
x
a
+
b
）
?
（
a
-
x
b
）
的圖象是一條直線，則必有（　　）
A．
a
⊥
b
B．
a
∥
b
C．
|
a
|
=
|
b
|
D．
|
a
|
≠
|
b
|
組卷：81引用：19難度：0.9
解析
11．設兩個向量
a
=（λ+2，λ²-cos²α）和
b
=（m,
m
2
+sinα），其中λ，m,α為實數．若
a
=2
b
，則
λ
m
的取值范圍是（　　）
A．[-6，8] B．[4，8] C．[-6，1] D．（4，8]
組卷：224引用：4難度：0.5
解析
12．已知
a
=（1，n），
b
=（-1，n），若2
a
-
b
與
b
垂直，則|
a
|=（　　）
A．1 B．
2
C．2 D．4
組卷：577引用：39難度：0.9
解析
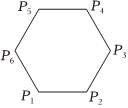13．如圖，已知正六邊形P₁P₂P₃P₄P₅P₆，下列向量的數量積中最大的是（　　）
A．
P
1
P
2
?
P
1
P
3
B．
P
1
P
2
?
P
1
P
4
C．
P
1
P
2
?
P
1
P
5
D．
P
1
P
2
?
P
1
P
6
組卷：664引用：27難度：0.9
解析
14．已知向量
a
≠
e
，|
e
|=1，對任意t∈R，恒有|
a
-t
e
|≥|
a
-
e
|，則（　　）
A．
a
⊥
e
B．
a
⊥（
a
-
e
）
C．
e
⊥（
a
-
e
） D．（
a
+
e
）⊥（
a
-
e
）
組卷：1262引用：22難度：0.9
解析
15．已知向量
OA
，
OB
的夾角為
π
3
，
|
OA
|
=
4
，
|
OB
|
=
1
，若點M在直線OB上，則
|
OA
-
OM
|
的最小值為（　　）
A．
3
B．
2
3
C．
6
D．
2
6
組卷：91引用：1難度：0.5
解析
16．在平行四邊形ABCD中，
AE
=
1
3
AB
，
AF
=
1
4
AD
，CE與BF相交于G點．若
AB
=
a
，
AD
=
b
，則
AG
=（　　）
A．
2
7
a
+
1
7
b
B．
2
7
a
+
3
7
b
C．
3
7
a
+
1
7
b
D．
4
7
a
+
2
7
b
組卷：330引用：5難度：0.9
解析
17．設向量
a
與
b
的夾角為θ，
a
=
（
2
，
1
）
，
a
+
2
b
=
（
4
，
5
）
，則cosθ等于（　　）
A．
10
10
B．
3
10
10
C．
3
5
D．
4
5
組卷：22引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題

52．設向量
a
=
（
1
，
cos
2
θ
）
，
b
=
（
2
，
1
）
，
c
=
（
4
sinθ
，
1
）
，
d
=
（
1
2
sinθ
，
1
）
，其中θ∈（0，
π
4
）．
（1）求
a
?
b
-
c
?
d
的取值范圍；
（2）若函數f（x）=|x-1|，比較f（
a
?
b
）與f（
c
?
d
）的大小．
組卷：146引用：20難度：0.3
解析
53．已知銳角△ABC三個內角分別為A，B，C向量
p
=
（
2
-
2
sin
A
，
cos
A
+
sin
A
）
與向量
q
=
（
sin
A
-
cos
A
，
1
+
sin
A
）
是共線向量．
（1）求∠A的值；
（2）求函數y=2sin²B+cos
C
-
3
B
2
的值域．
組卷：209引用：1難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．反向平行	B．同向平行
C．互相垂直	D．既不平行也不垂直

A． a ⊥ e	B． a ⊥（ a - e ）
C． e ⊥（ a - e ）	D．（ a + e ）⊥（ a - e ）

《第9章 平面向量》2013年單元測試卷

一、選擇題

1．設a、b、c是單位向量，且a?b=0，則（a-c）?（b-c）的最小值為（ ）

2．已知向量a=（2，1），a?b=10，|a+b|=52，則|b|=（ ）

3．平面向量a與b的夾角為60°，a=（2，0），|b|=1，則|a+2b|=（ ）

4．在△ABC中，M是BC的中點，AM=1，點P在AM上且滿足PA=-2PM，則PA?（PB+PC）等于（ ）

5．已知向量a=（-3，2），b=（-1，0），若λa+b與a-2b垂直，則實數λ的值為（ ）

6．設D、E、F分別是△ABC的三邊BC、CA、AB上的點，且DC=2BD，CE=2EA，AF=2FB，則AD+BE+CF與BC（ ）

7．已知a，b是平面內兩個互相垂直的單位向量，若向量c滿足（a-c）?（b-c）=0，則|c|的最大值是（ ）

8．已知O是△ABC所在平面內一點，D為BC邊中點，且2OA+OB+OC=0，那么（ ）

9．設a=（4，3），a在b上的投影為522，b在x軸上的投影為2，且|b|≤14，則b為（ ）

10．設a，b是非零向量，若函數f（x）=（xa+b）?（a-xb）的圖象是一條直線，則必有（ ）

11．設兩個向量a=（λ+2，λ2-cos2α）和b=（m,m2+sinα），其中λ，m,α為實數．若a=2b，則λm的取值范圍是（ ）

12．已知a=（1，n），b=（-1，n），若2a-b與b垂直，則|a|=（ ）

13．如圖，已知正六邊形P1P2P3P4P5P6，下列向量的數量積中最大的是（ ）

14．已知向量a≠e，|e|=1，對任意t∈R，恒有|a-te|≥|a-e|，則（ ）

15．已知向量OA，OB的夾角為π3，|OA|=4，|OB|=1，若點M在直線OB上，則|OA-OM|的最小值為（ ）

16．在平行四邊形ABCD中，AE=13AB，AF=14AD，CE與BF相交于G點．若AB=a，AD=b，則AG=（ ）

17．設向量a與b的夾角為θ，a=（2，1），a+2b=（4，5），則cosθ等于（ ）

三、解答題

52．設向量a=（1，cos2θ），b=（2，1），c=（4sinθ，1），d=（12sinθ，1），其中θ∈（0，π4）．（1）求a?b-c?d的取值范圍；（2）若函數f（x）=|x-1|，比較f（a?b）與f（c?d）的大小．

53．已知銳角△ABC三個內角分別為A，B，C向量p=（2-2sinA，cosA+sinA）與向量q=（sinA-cosA，1+sinA）是共線向量．（1）求∠A的值；（2）求函數y=2sin2B+cosC-3B2的值域．

《第9章平面向量》2013年單元測試卷

1．設
a
、
b
、
c
是單位向量，且
a
?
b
=
0
，則
（
a
-
c
）
?
（
b
-
c
）
的最小值為（　　）

2．已知向量
a
=（2，1），
a
?
b
=10，|
a
+
b
|=
5
2
，則|
b
|=（　　）

3．平面向量
a
與
b
的夾角為60°，
a
=（2，0），|
b
|=1，則|
a
+2
b
|=（　　）

4．在△ABC中，M是BC的中點，AM=1，點P在AM上且滿足
PA
=
-
2
PM
，則
PA
?
（
PB
+
PC
）
等于（　　）

5．已知向量
a
=（-3，2），
b
=（-1，0），若λ
a
+
b
與
a
-2
b
垂直，則實數λ的值為（　　）

6．設D、E、F分別是△ABC的三邊BC、CA、AB上的點，且
DC
=
2
BD
，
CE
=
2
EA
，
AF
=
2
FB
，則
AD
+
BE
+
CF
與
BC
（　　）

7．已知
a
，
b
是平面內兩個互相垂直的單位向量，若向量
c
滿足（
a
-
c
）?（
b
-
c
）=0，則|
c
|的最大值是（　　）

8．已知O是△ABC所在平面內一點，D為BC邊中點，且
2
OA
+
OB
+
OC
=
0
，那么（　　）

9．設
a
=
（
4
，
3
）
，
a
在
b
上的投影為
5
2
2
，
b
在x軸上的投影為2，且
|
b
|
≤
14
，則
b
為（　　）

10．設
a
，
b
是非零向量，若函數
f
（
x
）
=
（
x
a
+
b
）
?
（
a
-
x
b
）
的圖象是一條直線，則必有（　　）

11．設兩個向量
a
=（λ+2，λ²-cos²α）和
b
=（m,
m
2
+sinα），其中λ，m,α為實數．若
a
=2
b
，則
λ
m
的取值范圍是（　　）

12．已知
a
=（1，n），
b
=（-1，n），若2
a
-
b
與
b
垂直，則|
a
|=（　　）

13．如圖，已知正六邊形P₁P₂P₃P₄P₅P₆，下列向量的數量積中最大的是（　　）

14．已知向量
a
≠
e
，|
e
|=1，對任意t∈R，恒有|
a
-t
e
|≥|
a
-
e
|，則（　　）

15．已知向量
OA
，
OB
的夾角為
π
3
，
|
OA
|
=
4
，
|
OB
|
=
1
，若點M在直線OB上，則
|
OA
-
OM
|
的最小值為（　　）

16．在平行四邊形ABCD中，
AE
=
1
3
AB
，
AF
=
1
4
AD
，CE與BF相交于G點．若
AB
=
a
，
AD
=
b
，則
AG
=（　　）

17．設向量
a
與
b
的夾角為θ，
a
=
（
2
，
1
）
，
a
+
2
b
=
（
4
，
5
）
，則cosθ等于（　　）

52．設向量
a
=
（
1
，
cos
2
θ
）
，
b
=
（
2
，
1
）
，
c
=
（
4
sinθ
，
1
）
，
d
=
（
1
2
sinθ
，
1
）
，其中θ∈（0，
π
4
）．
（1）求
a
?
b
-
c
?
d
的取值范圍；
（2）若函數f（x）=|x-1|，比較f（
a
?
b
）與f（
c
?
d
）的大小．

53．已知銳角△ABC三個內角分別為A，B，C向量
p
=
（
2
-
2
sin
A
，
cos
A
+
sin
A
）
與向量
q
=
（
sin
A
-
cos
A
，
1
+
sin
A
）
是共線向量．
（1）求∠A的值；
（2）求函數y=2sin²B+cos
C
-
3
B
2
的值域．