2023-2024學年廣東省廣州市天河中學高二（上）月考數學試卷

一、單選題（本大題共8小題，共40.0分.在每小題列出的選項中，選出符合題目的一項）

• 1．在直角坐標系中，直線x+

  3

  y-3=0的傾斜角是（　　）

  A．150°

  B．60°

  C．30°

  D．120°
  組卷：281引用：11難度：0.9

  解析

• 2．兩條平行直線3x+4y-10=0與ax+8y+11=0之間的距離為（　　）

  A． 31 5

  B． 31 10

  C． 23 5

  D． 23 10
  組卷：573引用：14難度：0.7

  解析

• 3．圓（x+1）²+（y-2）²=1上的動點P到直線3x-4y-9=0的最短距離為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：79引用：3難度：0.5

  解析

• 4．四棱錐P-ABCD中，

  AB

  =（2，-1，3），

  AD

  =（-2，1，0），

  AP

  =（3，-1，4），則這個四棱錐的高為（　　）

  A． 5 5

  B． 1 5

  C． 2 5

  D． 2 5 5
  組卷：389引用：11難度：0.7

  解析

• 5．唐代詩人李頎的詩《古從軍行》開頭兩句說：“白日登山望烽火，黃昏飲馬傍交河．”詩中隱含著一個有趣的數學問題——“將軍飲馬”問題，即將軍在觀望烽火之后從山腳下某處出發，先到河邊飲馬后再回到軍營，怎樣走才能使總路程最短？在平面直角坐標系中，設軍營所在位置為B（-1，-4），若將軍從點A（-1，2）處出發，河岸線所在直線方程為x+y=3．則“將軍飲馬”的最短總路程為（　　）

  A． 13

  B． 17

  C． 2 17

  D．10
  組卷：105引用：9難度：0.7

  解析

• 6．若圓M：x²+y²-2x-2y-2=0上只有三個點到直線x+y+a=0的距離為1，求a的取值（　　）

  A． ± 2

  B． ± 2 2

  C． - 2 ± 2 2

  D． - 2 ± 2
  組卷：155引用：5難度：0.6

  解析

• 7．當曲線y=-

  4

  -

  x

  2

  與直線kx-y+2k-4=0有兩個相異的交點時，實數k的取值范圍是（　　）

  A．（0， 3 4 ）

  B．（ 5 12 ， 3 4 ]

  C．（ 3 4 ，1]

  D．（ 3 4 ，+∞）
  組卷：205引用：12難度：0.7

  解析

四、解答題（本大題共6小題，共70.0分.解答應寫出文字說明，證明過程或演算步驟）

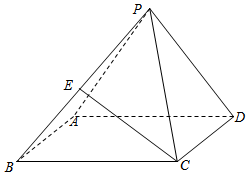• 21．在如圖所示的四棱錐P-ABCD中，底面ABCD是邊長為2的正方形，△PAD是正三角形，平面PAD⊥平面ABCD．
  （1）求平面PAB與平面PCD所成銳二面角的大小；
  （2）設E為PB上的動點，直線CE與平面PAB所成的角為θ，求sinθ的最大值．
  組卷：104引用：4難度：0.5

  解析

• 22．圓C的半徑為3，圓心C在直線2x+y=0上且在x軸下方，x軸被圓C截得的弦長為

  2

  5

  ．
  （1）求圓C的方程；
  （2）是否存在斜率為1的直線l,使得以l被圓C截得的弦AB為直徑的圓過原點？若存在，求出l的方程；若不存在，說明理由．
  組卷：479引用：17難度：0.5

  解析