當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年江蘇省蘇州市昆山市、太倉市、常熟市、張家港市八年級（上）期中數(shù)學(xué)試卷

發(fā)布：2024/10/10 8:0:2

一、選擇題：本大題共8小題，每小題3分，共24分.

1．在下列圖標(biāo)中，不是軸對稱圖形的是（　　）
A． B． C． D．
組卷：43引用：2難度：0.9
解析
2．下列各組數(shù)中，是勾股數(shù)的是（　　）
A．9，16，25 B．2，2，22 C．1，2，3 D．9，40，41
組卷：68引用：2難度：0.6
解析
3．2023年蘇州全市共有98516名考生參加了“蘇州市初中學(xué)業(yè)水平考試”，將數(shù)據(jù)98516精確到千位，并用科學(xué)記數(shù)法可表示為（　　）
A．99×10³ B．9.8×10⁴ C．9.9×10⁴ D．10.0×10⁴
組卷：42引用：1難度：0.8
解析
4．在實數(shù)
2
3
，
8
，
π
3
，3.14159中，無理數(shù)的個數(shù)有（　　）
A．1個 B．2個 C．3個 D．4個
組卷：46引用：1難度：0.8
解析
5．如圖，在△ABC中，∠C=90°，點D在邊AC上，連接BD，且∠DBC=60°，AD=BD，則∠A的度數(shù)為（　　）
A．15° B．18° C．20° D．25°
組卷：101引用：1難度：0.7
解析
6．實數(shù)與數(shù)軸上的點一一對應(yīng)，小明在構(gòu)造數(shù)軸上的點時，將一個直角邊長為1的等腰直角三角形放在數(shù)軸上，直角頂點C與原點重合，點A與數(shù)軸上表示-1的點重合．如圖，小明以點A為圓心，AB長為半徑畫弧，與數(shù)軸的負(fù)半軸交于點D，則點D表示的實數(shù)為（　　）
A．
-
2
B．
-
3
C．
-
1
-
2
D．
-
1
-
3
組卷：125引用：1難度：0.5
解析
7．小明把長度為10cm的鐵絲圍成三邊為整數(shù)長的等腰三角形，則圍成的等腰三角形的腰長為（　　）
A．3cm B．4cm C．2cm或4cm D．3cm或4cm
組卷：92引用：1難度：0.7
解析
8．如圖，在等腰三角形△ABC中，AB=AC，D為BC延長線上一點，EC⊥AC且AC=CE，垂足為C，連接BE，若BC=6，則△BCE的面積為（　　）
A．
9
2
B．9 C．18 D．36
組卷：1322引用：4難度：0.5
解析

二、填空題：本大題共8小題，每小題3分，共24分.把答案直接填在答題卷相應(yīng)位置上.

9．4的平方根是
．
組卷：844引用：15難度：0.9
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

三、解答題：本大題共11小題，共82分.把解答過程寫在答題卷相應(yīng)位置上，解答時應(yīng)寫出必

26．在△ABC中，
AB
=
AC
=
13
，BC=6，點P為邊BC上一動點，連接AP．
（1）BC邊上的高的長度為
；
（2）如圖1，若點P從點B出發(fā)，以每秒2個單位的速度向點C運動，設(shè)運動時間為t秒（0＜t＜3）．是否存在t值，使得△APC為等腰三角形？若存在，求出t的值；若不存在，請說明理由．
（3）如圖2，把△APB沿著直線AP翻折，點B的對應(yīng)點為點F，PF交邊AC于點E，當(dāng)AE=2EC時，求EF的長度．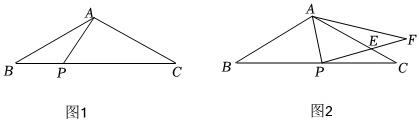
組卷：236引用：1難度：0.2
解析
27．定義：平面內(nèi)一點P到點A，點B，點C三個點的距離分別為PA、PB、PC，若有PA²+PB²=PC²，則稱點P為A，B，C三點關(guān)于點C的勾股點．
（1）若點P為A，B，C三點關(guān)于點C的勾股點，且PA=1，PB=2，則PC=
；
（2）如圖1，△ABC與△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC，AD=AE，點D為邊BC上一動點．求證：點D為B，C，E三點關(guān)于點E的勾股點；
（3）如圖2，△AEC為直角三角形，∠EAC=90°，點P為A，B，C三點關(guān)于點C的勾股點，連接PA，PC，作PD⊥AC，垂足為點B，交EC于點D，連接BE，且BE∥AP，AP=5，EC=8，試求BD的長度．
組卷：250引用：1難度：0.5
解析