2022-2023學年黑龍江省牡丹江第二高級中學高一（下）期末數學試卷

一、選擇題：本大題共8小題；每小題5分，共40分.在每小題給出的四個選項中，只有一個選項是符合題目要求的.

• 1．在復平面內，復數3i-2對應的點在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：49引用：3難度：0.9

  解析

• 2．在平行四邊形ABCD中，

  AB

  +

  AD

  等于（　　）

  A． AC

  B． BD

  C． BC

  D． CD
  組卷：509引用：3難度：0.9

  解析

• 3．已知向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  4

  ，

  m

  ）

  ，且

  a

  ⊥

  b

  ，則m=（　　）

  A．8

  B．2

  C．-2

  D．-8
  組卷：300引用：6難度：0.8

  解析

• 4．若

  a

  =（2，0，1），

  b

  =（-3，1，-1），

  c

  =（1，1，0），則

  a

  +2

  b

  -3

  c

  =（　　）

  A．（-1，-2，0）

  B．（-7，-1，0）

  C．（-7，-1，1）

  D．（-7，-1，-1）
  組卷：399引用：10難度：0.8

  解析

• 5．設正方體的棱長為

  3

  ，則它的外接球的表面積為（　　）

  A． 9 2 π

  B． 9 4 π

  C．9π

  D．3π
  組卷：101引用：2難度：0.7

  解析

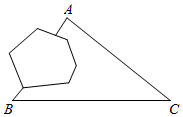• 6．如圖，在高速公路建設中，要確定隧道AB的長度，工程人員測得隧道兩端的A，B兩點到C點的距離分別為AC=3km,BC=4km,且∠ACB=60°，則隧道AB長度為（　　）

  A．2 2 km

  B． 11 km

  C．2 3 km

  D． 13 km
  組卷：149引用：2難度：0.8

  解析

• 7．下列命題中為真命題的是（　　）

  A．向量 AB 與 BA 的長度相等

  B．空間向量就是空間中的一條有向線段

  C．若將空間中所有的單位向量移到同一個起點，則它們的終點構成一個圓

  D．不相等的兩個空間向量的模必不相等
  組卷：132引用：7難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

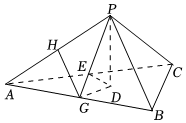• 21．如圖，已知正三棱錐P-ABC的側面是直角三角形，PA=6，頂點P在平面ABC內的正投影為點D，D在平面PAB內的正投影為點E，連接PE并延長交AB于點G．作GH∥PB交PA于H．
  （1）證明：G是AB的中點；
  （2）證明：GH⊥面PAC；
  （3）過點E作EF⊥面PAC，F為垂足，求三棱錐P-DEF的外接球體積．
  組卷：141引用：2難度：0.4

  解析

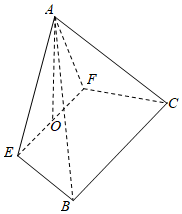• 22．如圖，將邊長為4的等邊三角形ABC沿與邊BC平行的直線EF折起，使得平面AEF⊥平面BCEF，O為EF的中點．
  （1）求平面AEF與平面AEB所成角的余弦值；
  （2）若BE⊥平面AOC，試求折痕EF的長；
  （3）當點O到平面ABC距離最大時，求折痕EF的長．
  組卷：273引用：5難度：0.3

  解析