當前位置：試卷中心 > 試卷詳情

2014-2015學年江西省新余四中高二（下）開學數學試卷（理科）

發布：2024/11/8 19:30:3

一、選擇題（本大題共12小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．已知a＞b＞0，那么下列不等式成立的是（　　）
A．-a＞-b B．a+c＜b+c
C．（-a）²＞（-b）² D．
1
a
＞
1
b
組卷：97引用：16難度：0.9
解析
2．已知△ABC中，
a
=
2
，
b
=
3
，B=60°，那么∠A=（　　）
A．45° B．90° C．135°或45° D．150°或30°
組卷：79引用：4難度：0.9
解析
3．設某批產品合格率為
3
4
，不合格率為
1
4
，現對該產品進行測試，設第ε次首次取到正品，則P（ε=3）等于（　　）
A．C₃²（
1
4
）²×（
3
4
） B．C₃²（
3
4
）²×（
1
4
）
C．（
1
4
）²×（
3
4
） D．（
3
4
）²×（
1
4
）
組卷：635引用：7難度：0.9
解析
4．不等式x+
2
x
+
1
＞2的解集是（　　）
A．（-1，0）∪（1，+∞） B．（-∞，-1）∪（0，1）
C．（-1，0）∪（0，1） D．（-∞，-1）∪（1，+∞）
組卷：332引用：19難度：0.9
解析
5．給出下面結論：
①命題p：“?x∈R，使x²-3x+2≥0”的否定為?p：“?x∈R，x²-3x+2＜0”；
②設X～N（μ，σ²），當σ逐漸變大時，其正態分布曲線越來越“高瘦”；
③當變量x,y的線性相關系數r＞0時，則線性回歸方程中的斜率b＞0；
④“M＞N”是“log₂M＞log₂N”的充分不必要條件．
其中正確結論的個數為（　　）
A．4 B．3 C．2 D．1
組卷：41引用：1難度：0.7
解析
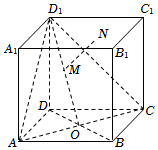6．如圖所示，正方體ABCD-A₁B₁C₁D₁的棱長為1，BD∩AC=O，M是線段D₁O上的動點，過點M作平面ACD₁的垂線交平面A₁B₁C₁D₁于點N，則點N到點A距離的最小值為（　　）
A．
2
B．
6
2
C．
2
3
3
D．1
組卷：276引用：11難度：0.9
解析
7．設x、y滿足約束條件
x
+
y
≤
1
y
≥
x
x
≥
0
，則z=2x+y的最大值為（　　）
A．0 B．
1
2
C．
3
2
D．3
組卷：14引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共6小題，共計70分．解答時應寫出必要的文字說明、證明過程或演算步驟．）

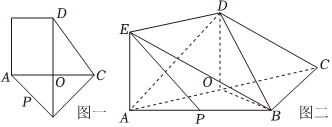21．在五邊形ABCDE中（圖一），BD是AC的垂直平分線，O為垂足．ED∥AC，AE∥BD，AB⊥BC，P為AB的中點．沿對角線AC將四邊形ACDE折起，使平面ACDE⊥平面ABC（圖二）．
（1）求證：PE∥平面DBC；
（2）當AB=
2
AE時，求直線DA與平面DBC所成角的正弦值．
組卷：62引用：4難度：0.5
解析
22．在數列{a_n}中，
a
1
=
5
，
a
n
+
1
=
3
a
n
+
2
n
+
1
（
n
∈
N
*
）

（1）求數列{a_n}的通項公式；
（2）令
b
n
=
2
n
+
1
3
n
+
1
-
a
n
，求數列{b_n}的前n項和s_n；
（3）令
c
n
=
a
n
a
n
+
1
，數列{c_n}的前n項和T_n，求證：
T
n
＞
3
n
-
4
9
．
組卷：56引用：2難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．-a＞-b	B．a+c＜b+c
C．（-a）²＞（-b）²	D． 1 a ＞ 1 b

A．C₃²（ 1 4 ）²×（ 3 4 ）	B．C₃²（ 3 4 ）²×（ 1 4 ）
C．（ 1 4 ）²×（ 3 4 ）	D．（ 3 4 ）²×（ 1 4 ）

A．（-1，0）∪（1，+∞）	B．（-∞，-1）∪（0，1）
C．（-1，0）∪（0，1）	D．（-∞，-1）∪（1，+∞）

2014-2015學年江西省新余四中高二（下）開學數學試卷（理科）

一、選擇題（本大題共12小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．已知a＞b＞0，那么下列不等式成立的是（ ）

2．已知△ABC中，a=2，b=3，B=60°，那么∠A=（ ）

3．設某批產品合格率為34，不合格率為14，現對該產品進行測試，設第ε次首次取到正品，則P（ε=3）等于（ ）

4．不等式x+2x+1＞2的解集是（ ）

6．如圖所示，正方體ABCD-A1B1C1D1的棱長為1，BD∩AC=O，M是線段D1O上的動點，過點M作平面ACD1的垂線交平面A1B1C1D1于點N，則點N到點A距離的最小值為（ ）

7．設x、y滿足約束條件x+y≤1y≥xx≥0，則z=2x+y的最大值為（ ）

三、解答題（本大題共6小題，共計70分．解答時應寫出必要的文字說明、證明過程或演算步驟．）

22．在數列{an}中，a1=5，an+1=3an+2n+1（n∈N*）（1）求數列{an}的通項公式；（2）令bn=2n+13n+1-an，求數列{bn}的前n項和sn；（3）令cn=anan+1，數列{cn}的前n項和Tn，求證：Tn＞3n-49．

1．已知a＞b＞0，那么下列不等式成立的是（　　）

2．已知△ABC中，
a
=
2
，
b
=
3
，B=60°，那么∠A=（　　）

3．設某批產品合格率為
3
4
，不合格率為
1
4
，現對該產品進行測試，設第ε次首次取到正品，則P（ε=3）等于（　　）

4．不等式x+
2
x
+
1
＞2的解集是（　　）

6．如圖所示，正方體ABCD-A₁B₁C₁D₁的棱長為1，BD∩AC=O，M是線段D₁O上的動點，過點M作平面ACD₁的垂線交平面A₁B₁C₁D₁于點N，則點N到點A距離的最小值為（　　）

7．設x、y滿足約束條件
x
+
y
≤
1
y
≥
x
x
≥
0
，則z=2x+y的最大值為（　　）

22．在數列{a_n}中，
a
1
=
5
，
a
n
+
1
=
3
a
n
+
2
n
+
1
（
n
∈
N
*
）

（1）求數列{a_n}的通項公式；
（2）令
b
n
=
2
n
+
1
3
n
+
1
-
a
n
，求數列{b_n}的前n項和s_n；
（3）令
c
n
=
a
n
a
n
+
1
，數列{c_n}的前n項和T_n，求證：
T
n
＞
3
n
-
4
9
．