2023-2024學年上海市閔行區(qū)文綺中學高三（上）期中數(shù)學試卷

一、填空題

• 1．已知集合M={-1，0，1，2}，N=（-1，1），則M∩N=

  ．
  組卷：7引用：1難度：0.8

  解析

• 2．不等式|x-1|≤1的解集為

  ．
  組卷：58引用：3難度：0.7

  解析

• 3．若“x=1”是“x＞a”的充分條件，則實數(shù)a的取值范圍為

  ．
  組卷：433引用：8難度：0.9

  解析

• 4．2022年世界杯亞洲區(qū)預選賽，中國和日本、澳大利亞、越南、阿曼、沙特阿拉伯分在同一小組，任意兩個國家需要在各自主場進行一場比賽，則該小組共有

  場比賽．
  組卷：123引用：3難度：0.8

  解析

• 5．若角α的終邊過點P（4，-3），則

  sin

  （

  3

  π

  2

  +

  α

  ）

  =

  ．
  組卷：1214引用：10難度：0.9

  解析

• 6．

  （

  x

  +

  1

  x

  ）

  n

  （n為正整數(shù)）的二項展開式中，若第三項與第五項的系數(shù)相等，則展開式中的常數(shù)項為

  ．
  組卷：128引用：6難度：0.9

  解析

• 7．已知

  sin

  （

  α

  +

  π

  12

  ）

  =

  3

  5

  ，則

  cos

  （

  2

  α

  +

  π

  6

  ）

  =

  ．
  組卷：276引用：6難度：0.9

  解析

三、解答題

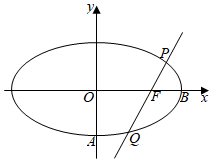• 20．已知橢圓方程

  x

  2

  2

  +

  y

  2

  =

  1

  右焦點F、斜率為k的直線l交橢圓于P、Q兩點．
  （1）求橢圓的兩個焦點和短軸的兩個端點構成的四邊形的面積；
  （2）當直線l的斜率為1時，求△POQ的面積；
  （3）在線段OF上是否存在點M（m,0），使得以MP、MQ為鄰邊的平行四邊形是菱形？若存在，求出m的取值范圍；若不存在，說明理由．
  組卷：520引用：10難度：0.5

  解析

• 21．已知數(shù)列{a_n}，若{a_n+a_n+1}為等比數(shù)列，則稱{a_n}具有性質P．
  （1）若數(shù)列{a_n}具有性質P，且a₁=a₂=1，a₃=3，求a₄、a₅的值；
  （2）若b_n=2ⁿ+（-1）ⁿ，判斷數(shù)列{b_n}是否具有性質P并證明；
  （3）設c₁+c₂+?+c_n=n²+n,數(shù)列{d_n}具有性質P，其d₁=1，d₃-d₂=c₁，d₂+d₃=c₂，試求數(shù)列{d_n}的通項公式．
  組卷：119引用：7難度：0.5

  解析