當前位置：試卷中心 > 試卷詳情

2016-2017學年四川省成都市龍泉一中高二（上）入學數學試卷（理科）

發布：2024/4/20 14:35:0

一、選擇題：共12小題，每小題5分，共60分．在每個小題給出的四個選項中，只有一項是符合題目要求的一項．

1．若點（1，a）到直線y=x+1的距離是
3
2
2
，則實數a為（　　）
A．-1 B．5 C．-1或5 D．-3或3
組卷：291引用：4難度：0.9
解析
2．已知平面向量
a
，
b
，
c
，下列命題正確的是（　　）
A．若
a
=
b
，
b
=
c
，則
a
=
c
B．若|
a
|=|
b
|，則
a
=
b
C．若λ
a
=
0
（λ為實數），則λ=0
D．若
a
∥
b
，
b
∥
c
，則
a
∥
c
組卷：325引用：2難度：0.9
解析
3．如圖所給的程序運行結果為S=35，那么判斷框中應填入的關于k的條件是（　　）
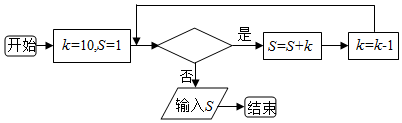
A．k=7 B．k≤6 C．k＜6 D．k＞6
組卷：189引用：41難度：0.7
解析
4．已知a,b,c∈R，則下列推證中正確的是（　　）
A．a＞b?am²＞bm² B．
a
c
＞
b
c
?
a
＞
b
C．
a
3
＞
b
3
，
ab
＞
0
?
1
a
＜
1
b
D．
a
2
＞
b
2
，
ab
＞
0
?
1
a
＜
1
b
組卷：403引用：36難度：0.7
解析
5．登山族為了了解某山高y（km）與氣溫x（℃）之間的關系，隨機統計了4次山高與相應的氣溫，并制作了對照表：

氣溫x（℃） 18 13 10 -1

山高y（km） 24 34 38 64

由表中數據，得到線性回歸方程
?
y
=
-
2
x
+
?
a
（
?
a
∈
R
）
，由此請估計出山高為72（km）處氣溫的度數為（　　）
A．-10℃ B．-8℃ C．-4℃ D．-6℃
組卷：395引用：18難度：0.9
解析
6．過點（-2，5）且垂直于直線2x-4y+15=0的直線方程為（　　）
A．2x+y-1=0 B．2x+y-5=0 C．x+2y-5=0 D．x-2y+7=0
組卷：110引用：2難度：0.9
解析
7．已知⊙C的圓心在曲線y=
2
x
上，⊙C過坐標原點O，且與x軸、y軸交于A、B兩點，則△OAB的面積是（　　）
A．2 B．3 C．4 D．8
組卷：87引用：3難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共6個小題，共70分．解答應寫出文字說明，證明過程或演算步驟）

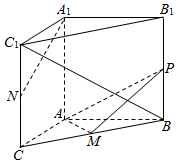21．如圖，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，∠BAC=90°，AB=AC=2，
A
A
1
=
3
．M，N分別為BC和CC₁的中點，P為側棱BB₁上的動點．
（Ⅰ）求證：平面APM⊥平面BB₁C₁C；
（Ⅱ）若P為線段BB₁的中點，求證：A₁N∥平面APM；
（Ⅲ）試判斷直線BC₁與平面APM是否能夠垂直．若能垂直，求PB的值；若不能垂直，請說明理由．
組卷：400引用：7難度：0.3
解析
22．已知定義在（-∞，0）∪（0，+∞）上的奇函數f（x）滿足f（2）=0，且在（-∞，0）上是增函數；又定義行列式
a
1
a
2
a
3
a
4
=
a
1
a
4
-
a
2
a
3
；函數
g
（
θ
）
=
sinθ
3
-
cosθ
m
sinθ
（其中
0
≤
θ
≤
π
2
）．
（1）若函數g（θ）的最大值為4，求m的值．
（2）若記集合M={m|恒有g（θ）＞0}，N={m|恒有f[g（θ）]＜0}，求M∩N．
組卷：111引用：4難度：0.1
解析