2022年貴州省安順市平壩區(qū)中考數(shù)學模擬試卷（5月份）

一、選擇題(本大題共12小題,每小題3分,共36分。在每小題所給的四個選項中,有且只有一項是符合題目要求的)

• 1．下列實數(shù)中，是無理數(shù)的是（　　）

  A． 11 3

  B． 3 - 8

  C． 0 . 04

  D．π
  組卷：35引用：2難度：0.9

  解析

• 2．下列幾何體中，左視圖是三角形的是（　　）

  A．

  B．

  C．

  D．
  組卷：47引用：1難度：0.7

  解析

• 3．芝麻被稱為“八谷之冠”，是世界上最古老的油料作物之一，經(jīng)測算，一粒芝麻的質量約為0.00000201kg,將數(shù)據(jù)0.00000201用科學記數(shù)法表示為（　　）

  A．20.1×10-7

  B．2.01×10-6

  C．0.201×10-5

  D．2.01×10-8
  組卷：130引用：15難度：0.9

  解析

• 4．從2，3，3，4中隨機抽取一個數(shù)，抽到這組數(shù)據(jù)的眾數(shù)的概率是（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D．1
  組卷：76引用：1難度：0.9

  解析

• 5．如圖，在Rt△ABC中，∠C=90°，以頂點B為圓心，適當長為半徑畫弧，分別交AB，BC于點M，N，再分別以點M，N為圓心，大于

  1

  2

  MN的長為半徑畫弧，兩弧相交于點P，畫射線BP交AC于點D．若CD=3，則點D到AB的距離為（　　）

  A．5

  B．4

  C．3

  D．1
  組卷：32引用：1難度：0.7

  解析

• 6．鄭州市新冠肺炎疫情防控指揮部發(fā)布開展全市全員新冠病毒核酸檢測的通告，某小區(qū)有3000人需要進行核酸檢測，由于組織有序，居民也積極配合，實際上每小時檢測人數(shù)比原計劃增加50人，結果提前2小時完成檢測任務．假設原計劃每小時檢測x人，則依題意，可列方程為（　　）

  A． 3000 x + 2 = 3000 x + 50	B． 3000 x - 2 = 3000 x + 50
  C． 3000 x + 2 + 50 = 3000 x	D． 3000 x + 2 - 50 = 3000 x
  組卷：652引用：8難度：0.8

  解析

• 7．為慶祝共青團成立100周年，某班50名同學進行了團史知識競賽，測試成績統(tǒng)計如表所示，其中有兩個數(shù)據(jù)被遮蓋．下列關于成績的統(tǒng)計量中，與被遮蓋的數(shù)據(jù)無關的是（　　）
  

  成績/分	91	92	93	94	95	96	97	98	99	100
  人數(shù)	1	■	■	2	3	5	6	8	10	12

  A．平均數(shù)、方差	B．中位數(shù)、方差
  C．平均數(shù)、極差	D．中位數(shù)、眾數(shù)
  組卷：53引用：1難度：0.6

  解析

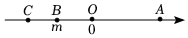• 8．已知點O，A，B，C在數(shù)軸上的位置如圖所示，O為原點，若BC=2，OA=OC，點B表示的數(shù)為m,則點A表示的數(shù)為（　　）

  A．m-2

  B．m+2

  C．-（m+2）

  D．-（ m-2）
  組卷：106引用：1難度：0.7

  解析

三、解答題（本大題共9小題，共98分。解答時應寫出必要的文字說明、證明過程或演算步驟）

• 24．如圖，拋物線y=ax²+bx+c經(jīng)過點A（-2，0），B（4，0），與y軸的正半軸交于點C，且OC=2OA，D是拋物線的頂點，對稱軸交x軸于點E．
  （1）求拋物線的函數(shù)解析式．
  （2）連接AC，若P是對稱軸右側、x軸上方的拋物線上一點，Q是直線BC上一點，是否存在以點E為直角頂點的Rt△PEQ，滿足tan∠EQP=tan∠OCA？若存在，請求出點P的坐標；若不存在，請說明理由．
  組卷：114引用：1難度：0.3

  解析

• 25．【問題情境】
  （1）如圖1，在正方形ABCD中，E，F(xiàn)，G分別是BC，AB，CD上的點，F(xiàn)G⊥AE于點Q．求證：AE=FG．
  【嘗試應用】
  （2）如圖2，正方形網(wǎng)格中，點A，B，C，D為格點，AB交CD于點O．求tan∠AOC的值；
  【拓展提升】
  （3）如圖3，點P是線段AB上的動點，分別以AP，BP為邊在AB的同側作正方形APCD與正方形PBEF，連接DE分別交線段BC，PC于點M，N．
  ①求∠DMC的度數(shù)；
  ②連接AC交DE于點H，直接寫出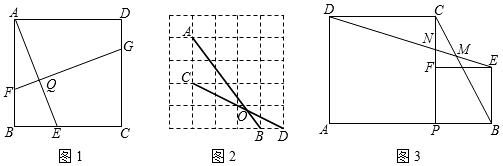

  DH

  BC

  的值．
  
  組卷：5568引用：13難度：0.2

  解析