2022-2023學年江西省宜春市宜豐中學高一（上）第二次月考數學試卷（11月份）

一、單選題（共40分）

• 1．已知集合A={x|ax²-3x+2=0}的元素只有一個，則實數a的值為（　　）

  A． 9 8

  B．0

  C． 9 8 或0

  D．無解
  組卷：477引用：4難度：0.7

  解析

• 2．已知p：

  x

  -

  1

  ＞

  2

  ，q：m-x＜0，若p是q的充分不必要條件，則m的取值范圍是（　　）

  A．m＜3

  B．m＞3

  C．m＜5

  D．m＞5
  組卷：423引用：11難度：0.7

  解析

• 3．已知函數

  f

  （

  x

  ）

  =

  x - 2 ， x ＞ 2

  | x - 3 | + 2 ， x ≤ 2

  ，則f（f（9））=（　　）

  A．1

  B．2

  C．4

  D．8
  組卷：78引用：3難度：0.7

  解析

• 4．函數

  f

  （

  x

  ）

  =

  x

  3

  2

  x

  +

  2

  -

  x

  的部分圖象大致為（　　）

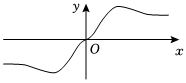
  A．	B．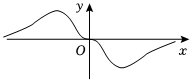
  C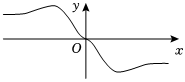．	D．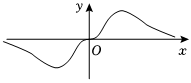
  組卷：135引用：7難度：0.8

  解析

• 5．設實數x滿足x＞0，函數y=2+3x+

  4

  x

  +

  1

  的最小值為（　　）

  A．4 3 -1

  B．4 3 +2

  C．4 2 +1

  D．6
  組卷：2047引用：10難度：0.7

  解析

• 6．若函數

  y

  =

  a

  x

  2

  +

  4

  x

  +

  1

  的值域為[0，+∞），則a的取值范圍為（　　）

  A．（0，4）

  B．（4，+∞）

  C．[0，4]

  D．[4，+∞）
  組卷：183引用：3難度：0.8

  解析

• 7．函數

  f

  （

  x

  ）

  =

  （

  6

  -

  x

  -

  x

  2

  ）

  3

  2

  的單調遞減區間為（　　）

  A． [ - 1 2 ， 2 ]

  B． [ - 3 ，- 1 2 ]

  C． [ - 1 2 ， + ∞ ）

  D． （ - ∞ ，- 1 2 ]
  組卷：821引用：5難度：0.9

  解析

四、解答題（70分）

• 21．設函數f（x）=ax²+（1-a）x+a-2．
  （1）若關于x的不等式f（x）≥-2有實數解，求實數a的取值范圍；
  （2）若不等式f（x）≥-2對于實數a∈[-1，1]時恒成立，求實數x的取值范圍．
  組卷：17引用：1難度：0.5

  解析

• 22．設函數f（x）=a^x-a^-x（x∈R，a＞0且a≠1）．
  （1）若f（1）＜0，求使不等式f（x²+tx）+f（4-x）＜0恒成立時實數t的取值范圍；
  （2）若

  f

  （

  1

  ）

  =

  3

  2

  ，

  g

  （

  x

  ）

  =

  a

  2

  x

  +

  a

  -

  2

  x

  -

  2

  mf

  （

  x

  ）

  且g（x）在[1，+∞）上的最小值為-2，求實數m的值．
  組卷：41引用：6難度：0.5

  解析